Refine listing
Actions for selected content:
1047 results in 60Fxx
A Diffusion Approximation for Markov Renewal Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 366-378
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Convolution Equivalence and Infinite Divisibility: Corrections and Corollaries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 295-305
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Tail Asymptotics of the Supremum of a Regenerative Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 349-365
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
On spatial thinning-replacement processes based on Voronoi cells
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 293-306
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Explicit laws of large numbers for random nearest-neighbour-type graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 326-342
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Inference in Lévy-type stochastic volatility models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 531-549
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Large deviation properties of constant rate data streams sharing a buffer with long-range dependent traffic in critical loading
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 407-428
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Tail Asymptotics for Monotone-Separable Networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 306-320
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
A weighted random walk model, with application to a genetic algorithm
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 550-568
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Arbitrary Threshold Widths for Monotone, Symmetric Properties
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 164-180
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Coupling of Two SIR Epidemic Models with Variable Susceptibilities and Infectivities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 41-57
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Stochastic stability of some state-dependent growth-collapse processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 189-220
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Renewal of singularity sets of random self-similar measures
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 162-188
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
A new genetic algorithm specifically based on mutation and selection
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 141-161
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Large Deviations Principle for Occupancy Problems with Colored Balls
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 115-141
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
On the asymptotic distribution of the discrete scan statistic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1137-1154
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Rate of convergence for the ‘square root formula’ in the Internet transmission control protocol
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 08 September 2016, pp. 1132-1154
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
On the asymptotic behaviour of random recursive trees in random environments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 08 September 2016, pp. 1047-1070
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Central limit theorems for generalized Pólya urn models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 938-951
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Critical sizing of LRU caches with dependent requests
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1013-1027
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
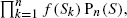 where the function
where the function 