Refine listing
Actions for selected content:
1047 results in 60Fxx
Large deviations for the leaves in some random trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 845-873
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Asymptotics of Implied Volatility far from Maturity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 629-650
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Convolutions of Long-Tailed and Subexponential Distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 756-767
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Aggregation of rapidly varying risks and asymptotic independence
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 797-828
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
A Central Limit Theorem Associated with the Transformed Two-Parameter Poisson–Dirichlet Distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 392-401
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
L Log L Criterion for a Class of Superdiffusions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 479-496
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
AN ALMOST SURE LIMIT THEOREM FOR THE MAXIMA OF MULTIVARIATE STATIONARY GAUSSIAN SEQUENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 01 June 2009, pp. 315-321
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Strong Laws for Balanced Triangular Urns
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 571-584
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
A fluid cluster Poisson input process can look like a fractional Brownian motion even in the slow growth aggregation regime
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 393-427
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Poisson Approximation in a Poisson Limit Theorem Inspired by Coupon Collecting
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 585-592
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
One-dimensional distributions of subordinators with upper truncated Lévy measure, and applications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 367-392
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
The speed of extinction for some generalized jiřina processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 576-599
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Bipower Variation for Gaussian Processes with Stationary Increments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 132-150
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Scan statistics of Lévy noises and marked empirical processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 13-37
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Primes with an average sum of digits
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 271-292
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Nearest-neighbor graphs on the cantor set
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 38-62
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Necklace Processes Via Pólya Urns
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 284-295
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Expected coalescence time for a nonuniform allocation process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1002-1032
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Large deviations for eigenvalues of sample covariance matrices, with applications to mobile communication systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1048-1071
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Tails of Stopped Random Products: The Factoid and Some Relatives
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1161-1180
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
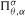 on the ordered infinite simplex. Furthermore, we prove the central limit theorem related to this distribution when both the mutation rate
on the ordered infinite simplex. Furthermore, we prove the central limit theorem related to this distribution when both the mutation rate 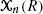 defined as the sum of marks of all points contained in
defined as the sum of marks of all points contained in 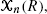 taken over all cubes
taken over all cubes 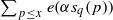 (where the sum is restricted to
(where the sum is restricted to 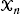 be a collection of
be a collection of 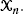 We prove convergence to a constant of the rescaled expected total edge length of this random graph. The rescaling factor is a function of the fractal dimension and has a log-periodic, nonconstant behavior.
We prove convergence to a constant of the rescaled expected total edge length of this random graph. The rescaling factor is a function of the fractal dimension and has a log-periodic, nonconstant behavior.