Refine listing
Actions for selected content:
1047 results in 60Fxx
A Central Limit Theorem and its Applications to Multicolor Randomly Reinforced Urns
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 527-546
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Exact Lower Bounds on the Exponential Moments of Truncated Random Variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 547-560
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
On the Maximal Offspring in a Critical Branching Process with Infinite Variance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 576-582
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Asymptotic normality for the number of records from general distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 422-436
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Hitting Times and the Running Maximum of Markovian Growth-Collapse Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 295-312
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Processes with Block-Associated Increments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 514-526
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Large deviations for a feed-forward network
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 545-571
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Asymptotic Properties of a Leader Election Algorithm
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 569-575
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
A weakly 1-stable distribution for the number of random records and cuttings in split trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 151-177
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Partial match queries in two-dimensional quadtrees: a probabilistic approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 178-194
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Extremal behavior of Archimedean copulas
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 195-216
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Limit theorems for supercritical age-dependent branching processes with neutral immigration
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 276-300
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Generalized Coupon Collection: The Superlinear Case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 189-199
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Sample Path Large Deviations for Order Statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 238-257
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
LARGE DEVIATIONS FOR INFINITE-DIMENSIONAL STOCHASTIC SYSTEMS WITH JUMPS
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 21 December 2010, pp. 175-192
- Print publication:
- January 2011
-
- Article
- Export citation
Limits of large metapopulations with patch-dependent extinction probabilities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1172-1186
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Second-order properties and central limit theory for the vertex process of iteration infinitely divisible and iteration stable random tessellations in the plane
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 913-935
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Information ranking and power laws on trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1057-1093
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
On customer flows in jackson queueing networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1094-1101
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
A Markov Model for the Spread of Viruses in an Open Population
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 976-996
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
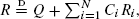 where
where 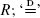 stands for equality in distribution. We study the asymptotic properties of the distribution of
stands for equality in distribution. We study the asymptotic properties of the distribution of 