Refine listing
Actions for selected content:
1047 results in 60Fxx
Upper Deviations for Split Times of Branching Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1134-1143
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Berry–Esseen Bounds and the Law of the Iterated Logarithm for Estimators of Parameters in an Ornstein–Uhlenbeck Process with Linear Drift
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 978-989
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Limit Theorems for Long-Memory Stochastic Volatility Models with Infinite Variance: Partial Sums and Sample Covariances
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1113-1141
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Asymptotics for Weighted Random Sums
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1142-1172
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
On the Functional Central Limit Theorem for Reversible Markov Chains with Nonlinear Growth of the Variance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1091-1105
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Quantitative Estimates for the Long-Time Behavior of an Ergodic Variant of the Telegraph Process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 977-994
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
A Pólya Approximation to the Poisson-Binomial Law
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 745-757
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
The Noisy Secretary Problem and Some Results on Extreme Concomitant Variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 821-837
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Probabilities of Competing Binomial Random Variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 731-744
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
The Class of Tenable Zero-Balanced Pólya Urn Schemes: Characterization and Gaussian Phases
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 702-728
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Piecewise-Deterministic Markov Processes as Limits of Markov Jump Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 729-748
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Fractional Brownian Motion with H < 1/2 as a Limit of Scheduled Traffic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 710-718
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Coalescence in Critical and Subcritical Galton-Watson Branching Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 627-638
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
A Central Limit Theorem for a Discrete-Time SIS Model with Individual Variation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 521-530
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Implicit Renewal Theory and Power Tails on Trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 528-561
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Stein's Method and Stochastic Orderings
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 343-372
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
On the Joint Behavior of Types of Coupons in Generalized Coupon Collection
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 429-451
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
A Self-Normalized Central Limit Theorem for Markov Random Walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 452-478
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Central Limit Theorems for Law-Invariant Coherent Risk Measures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 1-21
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Card Counting in Continuous Time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 184-198
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
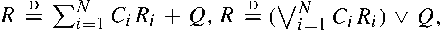 and similar recursions, where (
and similar recursions, where (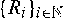 are independent and identically distributed copies of
are independent and identically distributed copies of 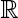 , and is adjoined to the chain such that {
, and is adjoined to the chain such that {