Refine listing
Actions for selected content:
1047 results in 60Fxx
On Large Deviations for Small Noise Itô Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 1126-1147
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
How did we get here?
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 63-72
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Projective Stochastic Equations and Nonlinear Long Memory
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 1084-1105
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A Binomial Splitting Process in Connection with Corner Parking Problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 971-989
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Extreme Analysis of a Random Ordinary Differential Equation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1021-1036
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A Quenched Central Limit Theorem for Reversible Random Walks in a Random Environment on Z
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1051-1064
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Minimal Clade Size in the Bolthausen-Sznitman Coalescent
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 657-668
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Limit Theory for High Frequency Sampled MCARMA Models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 846-877
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Limit Theorems for a Cox-Ingersoll-Ross Process with Hawkes Jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 699-712
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Existence and Uniqueness of a Quasistationary Distribution for Markov Processes with Fast Return from Infinity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 756-768
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
LIMIT THEOREMS FOR RADIAL RANDOM WALKS ON EUCLIDEAN SPACES OF HIGH DIMENSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 212-236
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
A Scaling Analysis of a Transient Stochastic Network
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 516-535
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
A New Two-Urn Model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 590-597
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Moments and Central Limit Theorems for Some Multivariate Poisson Functionals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 348-364
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
On the Asymmetric Telegraph Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 569-589
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Optimal Online Selection of an Alternating Subsequence: A Central Limit Theorem
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 536-559
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Improved Approximation of the Sum of Random Vectors by the Skew Normal Distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 466-482
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
On Asymptotics of the Beta Coalescents
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 496-515
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Tail Asymptotics of the Stationary Distribution of a Two-Dimensional Reflecting Random Walk with Unbounded Upward Jumps
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 365-399
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
The Limiting Behaviour of Hanski's Incidence Function Metapopulation Model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 297-316
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
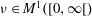
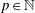
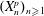
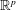

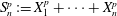

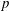

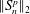
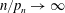
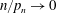
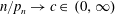
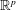
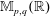
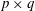
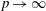
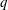
 .
.