Refine listing
Actions for selected content:
1047 results in 60Fxx
Extremes for the inradius in the Poisson line tessellation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 544-573
- Print publication:
- June 2016
-
- Article
- Export citation
A Galton–Watson process with a threshold
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 614-621
- Print publication:
- June 2016
-
- Article
- Export citation
On a memory game and preferential attachment graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 585-609
- Print publication:
- June 2016
-
- Article
- Export citation
Optimal importance sampling for the Laplace transform of exponential Brownian functionals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 531-542
- Print publication:
- June 2016
-
- Article
- Export citation
Convergence of directed random graphs to the Poisson-weighted infinite tree
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 463-474
- Print publication:
- June 2016
-
- Article
- Export citation
Shape theorems for Poisson hail on a bivariate ground
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 525-543
- Print publication:
- June 2016
-
- Article
- Export citation
On the invariance principle for reversible Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 593-599
- Print publication:
- June 2016
-
- Article
- Export citation
Shape Measures of Random Increasing k-trees†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 04 May 2016, pp. 668-699
-
- Article
- Export citation
Kloosterman paths and the shape of exponential sums
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 15 April 2016, pp. 1489-1516
- Print publication:
- July 2016
-
- Article
- Export citation
The speed of a random walk excited by its recent history
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 215-234
- Print publication:
- March 2016
-
- Article
- Export citation
Large deviations for multidimensional state-dependent shot-noise processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1097-1114
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Normal approximation for statistics of Gibbsian input in geometric probability
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 934-972
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
On degenerate sums of m-dependent variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1146-1155
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Generalized fractional Lévy processes with fractional Brownian motion limit
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 1108-1131
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Estimation of integrals with respect to infinite measures using regenerative sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1133-1145
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Records from stationary observations subject to a random trend
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 1175-1189
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
‘LIMITING BEHAVIOUR FOR ARRAYS OF UPPER EXTENDED NEGATIVELY DEPENDENT RANDOM VARIABLES’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 06 October 2015, p. 524
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Central limit theorem for a class of SPDEs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 786-796
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Large deviations for the Ornstein-Uhlenbeck process with shift
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 880-901
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Nonasymptotic performance analysis of importance sampling schemes for small noise diffusions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 797-810
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
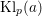

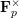
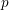
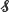 , π). We show that if a
, π). We show that if a 