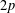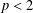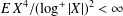Refine listing
Actions for selected content:
1047 results in 60Fxx
Optimal scaling of the random walk Metropolis algorithm under L p mean differentiability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1233-1260
- Print publication:
- December 2017
-
- Article
- Export citation
Central limit theorem for the Horton–Strahler bifurcation ratio of general branch order
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1111-1124
- Print publication:
- December 2017
-
- Article
- Export citation
Traffic flow densities in large transport networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 17 November 2017, pp. 1091-1115
- Print publication:
- December 2017
-
- Article
- Export citation
Fluid limit for the Poisson encounter-mating model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 17 November 2017, pp. 1201-1229
- Print publication:
- December 2017
-
- Article
- Export citation
Moderate deviations-based importance sampling for stochastic recursive equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 17 November 2017, pp. 981-1010
- Print publication:
- December 2017
-
- Article
- Export citation
Functional laws for trimmed Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 873-889
- Print publication:
- September 2017
-
- Article
- Export citation
Limit theorems for pure death processes coming down from infinity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 720-731
- Print publication:
- September 2017
-
- Article
- Export citation
Limit theorems for the zig-zag process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 791-825
- Print publication:
- September 2017
-
- Article
- Export citation
Dirichlet approximation of equilibrium distributions in Cannings models with mutation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 927-959
- Print publication:
- September 2017
-
- Article
- Export citation
Large deviation principle for epidemic models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 905-920
- Print publication:
- September 2017
-
- Article
- Export citation
Rare events of transitory queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 943-962
- Print publication:
- September 2017
-
- Article
- Export citation
Taylor's law, via ratios, for some distributions with infinite mean
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 657-669
- Print publication:
- September 2017
-
- Article
- Export citation
COMPLETE CONVERGENCE FOR ARRAYS AND THE LAW OF THE SINGLE LOGARITHM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 29 August 2017, pp. 333-344
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Subcritical Sevastyanov branching processes with nonhomogeneous Poisson immigration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 22 June 2017, pp. 569-587
- Print publication:
- June 2017
-
- Article
- Export citation
Path to survival for the critical branching processes in a random environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 22 June 2017, pp. 588-602
- Print publication:
- June 2017
-
- Article
- Export citation
Large deviations for the stochastic predator–prey model with nonlinear functional response
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 22 June 2017, pp. 507-521
- Print publication:
- June 2017
-
- Article
- Export citation
Second-order limit laws for occupation times of fractional Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 22 June 2017, pp. 444-461
- Print publication:
- June 2017
-
- Article
- Export citation
Moderate deviation principles for importance sampling estimators of risk measures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 22 June 2017, pp. 490-506
- Print publication:
- June 2017
-
- Article
- Export citation
Limit theorems associated with the Pitman–Yor process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 26 June 2017, pp. 581-602
- Print publication:
- June 2017
-
- Article
- Export citation
Joint degree distributions of preferential attachment random graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 26 June 2017, pp. 368-387
- Print publication:
- June 2017
-
- Article
- Export citation