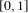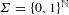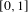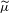Refine listing
Actions for selected content:
1047 results in 60Fxx
Approximation of the difference of two Poisson-like counts by Skellam
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 416-430
- Print publication:
- June 2018
-
- Article
- Export citation
Asymptotic behavior for the Robbins–Monro process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 559-570
- Print publication:
- June 2018
-
- Article
- Export citation
A quenched central limit theorem for biased random walks on supercritical Galton–Watson trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 610-626
- Print publication:
- June 2018
-
- Article
- Export citation
On Seneta–Heyde scaling for a stable branching random walk
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 565-599
- Print publication:
- June 2018
-
- Article
- Export citation
Exact moderate and large deviations for linear random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 431-449
- Print publication:
- June 2018
-
- Article
- Export citation
Local asymptotics for the area under the random walk excursion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 600-620
- Print publication:
- June 2018
-
- Article
- Export citation
First-passage time asymptotics over moving boundaries for random walk bridges
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 627-651
- Print publication:
- June 2018
-
- Article
- Export citation
RANDOM SPARSE SAMPLING IN A GIBBS WEIGHTED TREE AND PHASE TRANSITIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 09 May 2018, pp. 65-116
- Print publication:
- January 2020
-
- Article
- Export citation
A SIMPLE PROOF OF THE STRONG LAW OF LARGE NUMBERS WITH RATES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 513-517
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Inhomogeneous random graphs, isolated vertices, and Poisson approximation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 112-136
- Print publication:
- March 2018
-
- Article
- Export citation
Stein's method for negatively associated random variables with applications to second-order stationary random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 196-215
- Print publication:
- March 2018
-
- Article
- Export citation
Functional limit theorems for the number of busy servers in a G/G/∞ queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 15-29
- Print publication:
- March 2018
-
- Article
- Export citation
A remark on positive sojourn times of symmetric processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 69-81
- Print publication:
- March 2018
-
- Article
- Export citation
Domains of attraction for positive and discrete tempered stable distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 30-42
- Print publication:
- March 2018
-
- Article
- Export citation
Multiple drawing multi-colour urns by stochastic approximation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 254-281
- Print publication:
- March 2018
-
- Article
- Export citation
A Note on Rényi's ‘Record’ Problem and Engel's Series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 363-369
-
- Article
- Export citation
ADDITIVE ENERGY AND THE METRIC POISSONIAN PROPERTY
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 19 June 2018, pp. 679-700
- Print publication:
- 2018
-
- Article
- Export citation
Uniform convergence of conditional distributions for absorbed one-dimensional diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 178-203
- Print publication:
- March 2018
-
- Article
- Export citation
Dependence between path-length and size in random digital trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1125-1143
- Print publication:
- December 2017
-
- Article
- Export citation
Null recurrence and transience of random difference equations in the contractive case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1089-1110
- Print publication:
- December 2017
-
- Article
- Export citation