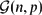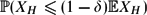Refine listing
Actions for selected content:
1047 results in 60Fxx
An extension of a convergence theorem for Markov chains arising in population genetics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 953-956
- Print publication:
- September 2016
-
- Article
- Export citation
One-component regular variation and graphical modeling of extremes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 733-746
- Print publication:
- September 2016
-
- Article
- Export citation
Computable bounds of an 𝓁²-spectral gap for discrete Markov chains with band transition matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 946-952
- Print publication:
- September 2016
-
- Article
- Export citation
Central limit theorems for a hypergeometric randomly reinforced urn
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 899-913
- Print publication:
- September 2016
-
- Article
- Export citation
Large deviations for the empirical measure of heavy-tailed Markov renewal processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 648-671
- Print publication:
- September 2016
-
- Article
- Export citation
On randomly spaced observations and continuous-time random walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 888-898
- Print publication:
- September 2016
-
- Article
- Export citation
Laplace transform asymptotics and large deviation principles for longest success runs in Bernoulli trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 747-764
- Print publication:
- September 2016
-
- Article
- Export citation
On large deviation rates for sums associated with Galton‒Watson processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 672-690
- Print publication:
- September 2016
-
- Article
- Export citation
On real growth and run-off companies in insurance ruin theory
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 903-925
- Print publication:
- September 2016
-
- Article
- Export citation
G/G/∞ queues with renewal alternating interruptions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 812-831
- Print publication:
- September 2016
-
- Article
- Export citation
Renewal approximation for the absorption time of a decreasing Markov chain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 765-782
- Print publication:
- September 2016
-
- Article
- Export citation
Coalescence on critical and subcritical multitype branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 802-817
- Print publication:
- September 2016
-
- Article
- Export citation
Risk minimization for game options in markets imposing minimal transaction costs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 926-946
- Print publication:
- September 2016
-
- Article
- Export citation
On the Lower Tail Variational Problem for Random Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 2 / March 2017
- Published online by Cambridge University Press:
- 16 August 2016, pp. 301-320
-
- Article
- Export citation
Existence of moments of a counting process and convergence in multidimensional time
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 181-201
- Print publication:
- July 2016
-
- Article
- Export citation
On the weak limit law of the maximal uniform k-spacing
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 235-238
- Print publication:
- July 2016
-
- Article
- Export citation
Degrees in random self-similar bipolar networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 434-447
- Print publication:
- June 2016
-
- Article
- Export citation
Convergence to the structured coalescent process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 502-517
- Print publication:
- June 2016
-
- Article
- Export citation
Marcinkiewicz law of large numbers for outer products of heavy-tailed, long-range dependent data
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 349-368
- Print publication:
- June 2016
-
- Article
- Export citation
Generalized Efron's biased coin design and its theoretical properties
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 327-340
- Print publication:
- June 2016
-
- Article
- Export citation