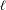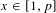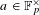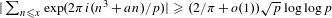Refine listing
Actions for selected content:
1047 results in 60Fxx
All solutions of the stochastic fixed point equation of the Quicksort process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 131-140
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Genealogical constructions and asymptotics for continuous-time Markov and continuous-state branching processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 197-209
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Weak convergence of the number of vertices at intermediate levels of random recursive trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1131-1142
- Print publication:
- December 2018
-
- Article
- Export citation
An asymmetric St. Petersburg game with trimming
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 115-129
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
The weak law of large numbers for nonnegative summands
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 241-252
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Pathwise large deviations for the rough Bergomi model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1078-1092
- Print publication:
- December 2018
-
- Article
- Export citation
Regular variation in a fixed-point problem for single- and multi-class branching processes and queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 47-61
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Linear de-preferential urn models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1176-1192
- Print publication:
- December 2018
-
- Article
- Export citation
Limit theorems for random polytopes with vertices on convex surfaces
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1227-1245
- Print publication:
- December 2018
-
- Article
- Export citation
ON THE DISTRIBUTION OF THE MAXIMUM OF CUBIC EXPONENTIAL SUMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 27 September 2018, pp. 1259-1286
- Print publication:
- July 2020
-
- Article
- Export citation
Approximation of excessive backlog probabilities of two tandem queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 968-997
- Print publication:
- September 2018
-
- Article
- Export citation
Reach of repulsion for determinantal point processes in high dimensions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 760-788
- Print publication:
- September 2018
-
- Article
- Export citation
Large deviations for randomly connected neural networks: II. State-dependent interactions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 983-1004
- Print publication:
- September 2018
-
- Article
- Export citation
Compound Poisson approximation of subgraph counts in stochastic block models with multiple edges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 759-782
- Print publication:
- September 2018
-
- Article
- Export citation
Multi-type branching processes with time-dependent branching rates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 701-727
- Print publication:
- September 2018
-
- Article
- Export citation
Large deviations for randomly connected neural networks: I. Spatially extended systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 944-982
- Print publication:
- September 2018
-
- Article
- Export citation
Relaxation of monotone coupling conditions: Poisson approximation and beyond
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 742-759
- Print publication:
- September 2018
-
- Article
- Export citation
Windings of planar processes, exponential functionals and Asian options
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 726-742
- Print publication:
- September 2018
-
- Article
- Export citation
Limit Shapes via Bijections
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 02 August 2018, pp. 187-240
-
- Article
- Export citation
Self-normalized large deviation for supercritical branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 450-458
- Print publication:
- June 2018
-
- Article
- Export citation