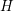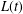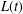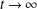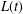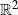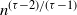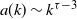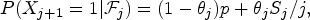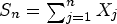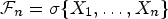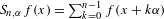Refine listing
Actions for selected content:
1047 results in 60Fxx
Insensitivity of the mean field limit of loss systems under SQ(d) routeing
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 November 2019, pp. 1027-1066
- Print publication:
- December 2019
-
- Article
- Export citation
ASYMPTOTIC EXPANSION OF THE DENSITY FOR HYPOELLIPTIC ROUGH DIFFERENTIAL EQUATION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 04 November 2019, pp. 11-41
- Print publication:
- September 2021
-
- Article
- Export citation
LARGE DEVIATIONS FOR THE LONGEST GAP IN POISSON PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 16 October 2019, pp. 146-156
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
SOME LIMIT THEOREMS OF DELAYED AVERAGES FOR COUNTABLE NONHOMOGENEOUS MARKOV CHAINS
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 35 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 24 September 2019, pp. 297-315
-
- Article
- Export citation
Scaling limits for a random boxes model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 September 2019, pp. 773-801
- Print publication:
- September 2019
-
- Article
- Export citation
Degree correlations in scale-free random graph models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 672-700
- Print publication:
- September 2019
-
- Article
- Export citation
Subgraphs in preferential attachment models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 September 2019, pp. 898-926
- Print publication:
- September 2019
-
- Article
- Export citation
Branching Brownian motion with spatially homogeneous and point-catalytic branching
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 891-917
- Print publication:
- September 2019
-
- Article
- Export citation
The exact asymptotics of the large deviation probabilities in the multivariate boundary crossing problem
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 September 2019, pp. 835-864
- Print publication:
- September 2019
-
- Article
- Export citation
Robust Wasserstein profile inference and applications to machine learning
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 830-857
- Print publication:
- September 2019
-
- Article
- Export citation
Limit theorems for multivariate Brownian semistationary processes and feasible results
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 September 2019, pp. 667-716
- Print publication:
- September 2019
-
- Article
- Export citation
Limit theorems for some skew products with mixing base maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 05 August 2019, pp. 241-271
- Print publication:
- January 2021
-
- Article
- Export citation
ASYMPTOTIC BEHAVIORS FOR CORRELATED BERNOULLI MODEL
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 570-582
-
- Article
- Export citation
Fast and slow points of Birkhoff sums
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 3236-3256
- Print publication:
- December 2020
-
- Article
- Export citation
On the total claim amount for marked Poisson cluster models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 541-569
- Print publication:
- June 2019
-
- Article
- Export citation
The limit distribution of the maximum probability nearest-neighbour ball
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 574-589
- Print publication:
- June 2019
-
- Article
- Export citation
On the rate of convergence for the length of the longest common subsequences in hidden Markov models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 558-573
- Print publication:
- June 2019
-
- Article
- Export citation
The De Vylder–Goovaerts conjecture holds within the diffusion limit
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 546-557
- Print publication:
- June 2019
-
- Article
- Export citation
Accessibility percolation on random rooted labeled trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 533-545
- Print publication:
- June 2019
-
- Article
- Export citation
Asymptotic behaviour of randomised fractional volatility models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 496-523
- Print publication:
- June 2019
-
- Article
- Export citation