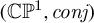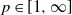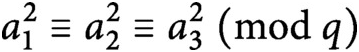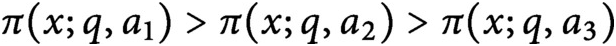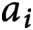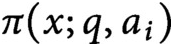Refine listing
Actions for selected content:
1046 results in 60Fxx
Functional limit theorems for the euler characteristic process in the critical regime
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 March 2021, pp. 57-80
- Print publication:
- March 2021
-
- Article
- Export citation
Long-Time Trajectorial Large Deviations and Importance Sampling for Affine Stochastic Volatility Models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 March 2021, pp. 220-250
- Print publication:
- March 2021
-
- Article
- Export citation
Diffusion approximations for randomly arriving expert opinions in a financial market with Gaussian drift
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 197-216
- Print publication:
- March 2021
-
- Article
- Export citation
Tail asymptotics for the area under the excursion of a random walk with heavy-tailed increments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 217-237
- Print publication:
- March 2021
-
- Article
- Export citation
Gaussian process approximations for multicolor Pólya urn models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 274-286
- Print publication:
- March 2021
-
- Article
- Export citation
RANDOM REAL BRANCHED COVERINGS OF THE PROJECTIVE LINE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 1783-1799
- Print publication:
- September 2022
-
- Article
- Export citation
Large deviations for a class of tempered subordinators and their inverse processes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 2030-2050
- Print publication:
- December 2021
-
- Article
- Export citation
Limit theorems for multi-type general branching processes with population dependence
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1127-1163
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
Mean and variance of balanced Pólya urns
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1224-1248
- Print publication:
- December 2020
-
- Article
- Export citation
Limit theorems for assortativity and clustering in null models for scale-free networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1035-1084
- Print publication:
- December 2020
-
- Article
- Export citation
Rate of convergence for traditional Pólya urns
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1029-1044
- Print publication:
- December 2020
-
- Article
- Export citation
Asymptotic normality in t-stack sortable permutations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 04 November 2020, pp. 1062-1070
-
- Article
- Export citation
Autocorrelation functions for quantum particles in supersymmetric Pöschl-Teller potentials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 October 2020, pp. 840-852
- Print publication:
- December 2021
-
- Article
- Export citation
Densities in certain three-way prime number races
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 12 October 2020, pp. 232-265
- Print publication:
- February 2022
-
- Article
- Export citation
Large deviations and central limit theorems for sequential and random systems of intermittent maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 07 October 2020, pp. 2805-2832
- Print publication:
- September 2021
-
- Article
- Export citation
ON STATISTICAL PROPERTIES OF NONLINEAR FUNCTIONALS OF RANDOM FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 18 September 2020, pp. 338-340
- Print publication:
- April 2021
-
- Article
-
- You have access
- Export citation
Almost sure central limit theorems in stochastic geometry
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 705-734
- Print publication:
- September 2020
-
- Article
- Export citation
Decorrelation of a class of Gibbs particle processes and asymptotic properties of U-statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 928-955
- Print publication:
- September 2020
-
- Article
- Export citation
Out-of-equilibrium random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 772-797
- Print publication:
- September 2020
-
- Article
- Export citation
Strong convergence of infinite color balanced urns under uniform ergodicity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 853-865
- Print publication:
- September 2020
-
- Article
- Export citation