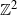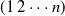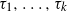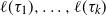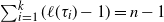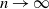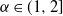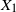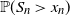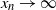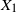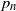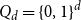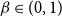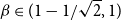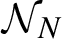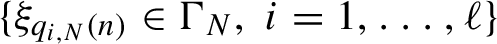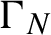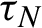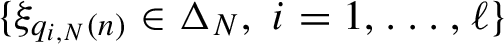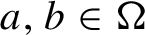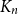Refine listing
Actions for selected content:
1047 results in 60Fxx
Limit theorems and structural properties of the cat-and-mouse Markov chain and its generalisations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 141-166
- Print publication:
- March 2022
-
- Article
- Export citation
Kingman’s model with random mutation probabilities: convergence and condensation I
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 25 February 2022, pp. 311-335
- Print publication:
- March 2022
-
- Article
- Export citation
Random stable-type minimal factorizations of the n-cycle
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 24 February 2022, pp. 1-63
- Print publication:
- March 2022
-
- Article
- Export citation
ON MODERATE DEVIATIONS FOR COUNT DATA AND GAMMA APPROXIMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 347-348
- Print publication:
- April 2022
-
- Article
-
- You have access
- HTML
- Export citation
Large-deviation results for triangular arrays of semiexponential random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 399-420
- Print publication:
- June 2022
-
- Article
- Export citation
Random Young towers and quenched limit laws
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 03 February 2022, pp. 971-1003
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prevalence of deficiency-zero reaction networks in an Erdös–Rényi framework
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 28 January 2022, pp. 384-398
- Print publication:
- June 2022
-
- Article
- Export citation
On the asymptotic behavior of the Diaconis–Freedman chain in a multi-dimensional simplex
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 28 January 2022, pp. 505-526
- Print publication:
- June 2022
-
- Article
- Export citation
Rate of strong convergence to Markov-modulated Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 1-16
- Print publication:
- March 2022
-
- Article
- Export citation
The containment profile of hyper-recursive trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 278-296
- Print publication:
- March 2022
-
- Article
- Export citation
Asymptotics of quasi-stationary distributions of small noise stochastic dynamical systems in unbounded domains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 64-110
- Print publication:
- March 2022
-
- Article
- Export citation
Independent sets of a given size and structure in the hypercube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 702-720
-
- Article
- Export citation
Large deviation principle for piecewise monotonic maps with density of periodic measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 14 December 2021, pp. 861-872
- Print publication:
- March 2023
-
- Article
- Export citation
Large-deviation asymptotics of condition numbers of random matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1114-1130
- Print publication:
- December 2021
-
- Article
- Export citation
A restaurant process with cocktail bar and relations to the three-parameter Mittag–Leffler distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 978-1006
- Print publication:
- December 2021
-
- Article
- Export citation
Two poisson limit theorems for the coupon collector’s problem with group drawings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 966-977
- Print publication:
- December 2021
-
- Article
- Export citation
Asymptotic behavior of projections of supercritical multi-type continuous-state and continuous-time branching processes with immigration
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1023-1060
- Print publication:
- December 2021
-
- Article
- Export citation
Large deviation principles of 2D stochastic Navier–Stokes equations with Lévy noises
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 18 November 2021, pp. 19-67
- Print publication:
- February 2023
-
- Article
- Export citation
Limit theorems for numbers of multiple returns in non-conventional arrays
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 12 November 2021, pp. 1098-1121
- Print publication:
- March 2022
-
- Article
- Export citation
On bucket increasing trees, clustered increasing trees and increasing diamonds
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 13 October 2021, pp. 629-661
-
- Article
- Export citation