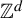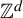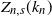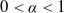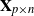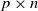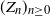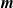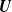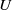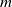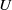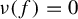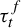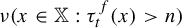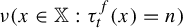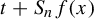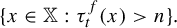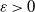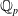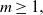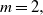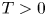Refine listing
Actions for selected content:
1046 results in 60Fxx
Distribution of consensus in a broadcast-based consensus algorithm with random initial opinions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 09 May 2023, pp. 1416-1438
- Print publication:
- December 2023
-
- Article
- Export citation
Decomposition of multicorrelation sequences and joint ergodicity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 04 May 2023, pp. 432-480
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mixing time bounds for edge flipping on regular graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 1317-1332
- Print publication:
- December 2023
-
- Article
- Export citation
Approaching the coupon collector’s problem with group drawings via Stein’s method
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 25 April 2023, pp. 1352-1366
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
Large deviations of extremal eigenvalues of sample covariance matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1275-1280
- Print publication:
- December 2023
-
- Article
- Export citation
Limiting shape for first-passage percolation models on random geometric graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1367-1385
- Print publication:
- December 2023
-
- Article
- Export citation
Self-normalized Cramér moderate deviations for a supercritical Galton–Watson process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1281-1292
- Print publication:
- December 2023
-
- Article
- Export citation
Local limits of spatial inhomogeneous random graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 14 April 2023, pp. 793-840
- Print publication:
- September 2023
-
- Article
- Export citation
Breaking of ensemble equivalence for dense random graphs under a single constraint
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1181-1200
- Print publication:
- December 2023
-
- Article
- Export citation
Stein’s method and approximating the multidimensional quantum harmonic oscillator
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 855-873
- Print publication:
- September 2023
-
- Article
-
- You have access
- HTML
- Export citation
How do empirical estimators of popular risk measures impact pro-cyclicality?
- Part of
-
- Journal:
- Annals of Actuarial Science / Volume 17 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 29 March 2023, pp. 547-579
-
- Article
- Export citation
Asymptotic normality for
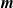 $\boldsymbol{m}$-dependent and constrained
$\boldsymbol{m}$-dependent and constrained 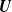 $\boldsymbol{U}$-statistics, with applications to pattern matching in random strings and permutations
$\boldsymbol{U}$-statistics, with applications to pattern matching in random strings and permutations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 28 March 2023, pp. 841-894
- Print publication:
- September 2023
-
- Article
- Export citation
Conditioned limit theorems for hyperbolic dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 50-117
- Print publication:
- January 2024
-
- Article
- Export citation
A central limit theorem for conservative fragmentation chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 17 March 2023, pp. 1031-1068
- Print publication:
- September 2023
-
- Article
- Export citation
An ergodic theorem for asymptotically periodic time-inhomogeneous Markov processes, with application to quasi-stationarity with moving boundaries
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 March 2023, pp. 672-700
- Print publication:
- June 2023
-
- Article
- Export citation
Gaps between prime divisors and analogues in Diophantine geometry
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. S129-S147
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sojourn functionals for spatiotemporal Gaussian random fields with long memory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 09 February 2023, pp. 148-165
- Print publication:
- March 2023
-
- Article
- Export citation
Multiple-drawing dynamic Friedman urns with opposite-reinforcement
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 26 January 2023, pp. 115-129
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence of blanket times for sequences of random walks on critical random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 09 January 2023, pp. 478-515
-
- Article
- Export citation
Asymptotics of a time bounded cylinder model
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 27 December 2022, pp. 1063-1083
-
- Article
-
- You have access
- Open access
- HTML
- Export citation