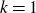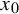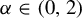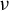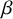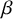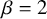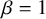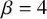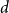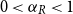Refine listing
Actions for selected content:
1046 results in 60Fxx
Depths in random recursive metric spaces
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1448-1462
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Branching processes in nearly degenerate varying environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1107-1126
- Print publication:
- December 2024
-
- Article
- Export citation
The Ulam–Hammersley problem for multiset permutations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 09 May 2024, pp. 23-48
- Print publication:
- July 2024
-
- Article
- Export citation
Topological reconstruction of compact supports of dependent stationary random variables
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1339-1369
- Print publication:
- December 2024
-
- Article
- Export citation
A sufficient condition for the quasipotential to be the rate function of the invariant measure of countable-state mean-field interacting particle systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 21 March 2024, pp. 960-1003
- Print publication:
- September 2024
-
- Article
- Export citation
Asymptotic results for sums and extremes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 13 March 2024, pp. 1153-1171
- Print publication:
- December 2024
-
- Article
- Export citation
Invariant measures and large deviation principles for stochastic Schrödinger delay lattice systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1813-1854
- Print publication:
- October 2025
-
- Article
- Export citation
Average Jaccard index of random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1139-1152
- Print publication:
- December 2024
-
- Article
- Export citation
Inference on the intraday spot volatility from high-frequency order prices with irregular microstructure noise
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 14 February 2024, pp. 858-885
- Print publication:
- September 2024
-
- Article
- Export citation
Stable laws for random dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 14 February 2024, pp. 3041-3090
- Print publication:
- November 2024
-
- Article
- Export citation
An exponential nonuniform Berry–Esseen bound of the maximum likelihood estimator in a Jacobi process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 14 February 2024, pp. 909-926
- Print publication:
- September 2024
-
- Article
- Export citation
Scaling limit of the local time of random walks conditioned to stay positive
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 13 February 2024, pp. 1060-1074
- Print publication:
- September 2024
-
- Article
- Export citation
Asymptotic expansion of
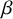 $\beta $ matrix models in the multi-cut regime
$\beta $ matrix models in the multi-cut regime
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 24 January 2024, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local weak limit of preferential attachment random trees with additive fitness
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 785-824
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Central limit theorem for a birth–growth model with poisson arrivals and random growth speed
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1004-1032
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp large deviations and concentration inequalities for the number of descents in a random permutation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 810-833
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Every complex Hénon map is exponentially mixing of all orders and satisfies the CLT
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 January 2024, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak convergence of the extremes of branching Lévy processes with regularly varying tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 December 2023, pp. 622-643
- Print publication:
- June 2024
-
- Article
- Export citation
On minimum spanning trees for random Euclidean bipartite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 319-350
-
- Article
- Export citation
A large-deviation principle for birth–death processes with a linear rate of downward jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 781-801
- Print publication:
- September 2024
-
- Article
- Export citation