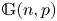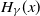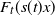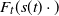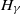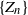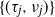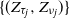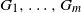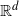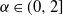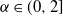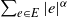Refine listing
Actions for selected content:
1046 results in 60Fxx
Central limit theorem in complete feedback games
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 16 October 2023, pp. 654-666
- Print publication:
- June 2024
-
- Article
- Export citation
Stochastic differential equation approximations of generative adversarial network training and its long-run behavior
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 465-489
- Print publication:
- June 2024
-
- Article
- Export citation
Fluctuations of the local times of the self-repelling random walk with directed edges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 September 2023, pp. 545-586
- Print publication:
- June 2024
-
- Article
- Export citation
Strong convergence of an epidemic model with mixing groups
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 01 September 2023, pp. 430-463
- Print publication:
- June 2024
-
- Article
- Export citation
MONTE CARLO VARIANCE REDUCTION METHODS WITH APPLICATIONS IN STRUCTURAL RELIABILITY ANALYSIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 31 August 2023, pp. 518-521
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
Subgraph distributions in dense random regular graphs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 25 August 2023, pp. 2125-2148
- Print publication:
- October 2023
-
- Article
- Export citation
Strong convergence of peaks over a threshold
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 23 August 2023, pp. 529-539
- Print publication:
- June 2024
-
- Article
- Export citation
Branching processes in random environments with thresholds
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 495-544
- Print publication:
- June 2024
-
- Article
- Export citation
Normal and stable approximation to subgraph counts in superpositions of Bernoulli random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 18 August 2023, pp. 401-419
- Print publication:
- June 2024
-
- Article
- Export citation
Heavy-traffic limits for parallel single-server queues with randomly split Hawkes arrival processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 07 August 2023, pp. 490-514
- Print publication:
- June 2024
-
- Article
- Export citation
Normal approximation in total variation for statistics in geometric probability
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 03 July 2023, pp. 106-155
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
 $\alpha$-Stable convergence of heavy-/light-tailed infinitely wide neural networks
$\alpha$-Stable convergence of heavy-/light-tailed infinitely wide neural networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 03 July 2023, pp. 1415-1441
- Print publication:
- December 2023
-
- Article
- Export citation
Information-theoretic convergence of extreme values to the Gumbel distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 21 June 2023, pp. 244-254
- Print publication:
- March 2024
-
- Article
- Export citation
On sparsity, power-law, and clustering properties of graphex processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 1211-1253
- Print publication:
- December 2023
-
- Article
- Export citation
Wasserstein convergence rates in the invariance principle for deterministic dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 June 2023, pp. 1172-1191
- Print publication:
- April 2024
-
- Article
- Export citation
Propagation of chaos and large deviations in mean-field models with jumps on block-structured networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 05 June 2023, pp. 1301-1361
- Print publication:
- December 2023
-
- Article
- Export citation
Homogenization of non-symmetric jump processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 1-33
- Print publication:
- March 2024
-
- Article
- Export citation
Upper large deviations for power-weighted edge lengths in spatial random networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 34-70
- Print publication:
- March 2024
-
- Article
- Export citation
Averaging for slow–fast piecewise deterministic Markov processes with an attractive boundary
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 19 May 2023, pp. 1439-1468
- Print publication:
- December 2023
-
- Article
- Export citation
On asymptotic fairness in voting with greedy sampling
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 May 2023, pp. 999-1032
- Print publication:
- September 2023
-
- Article
- Export citation