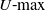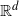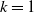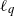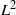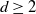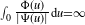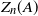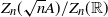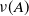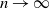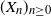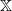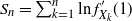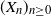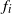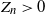Refine listing
Actions for selected content:
1046 results in 60Fxx
Interacting nonlinear reinforced stochastic processes: Synchronization or non-synchronization
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 275-320
- Print publication:
- March 2023
-
- Article
- Export citation
A note on the polynomial ergodicity of the one-dimensional Zig-Zag process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 18 July 2022, pp. 895-903
- Print publication:
- September 2022
-
- Article
- Export citation
Generalized limit theorems for U-max statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 825-848
- Print publication:
- September 2022
-
- Article
- Export citation
Asymptotics of the overflow in urn models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 797-824
- Print publication:
- September 2022
-
- Article
- Export citation
Large-time behaviour and the second eigenvalue problem for finite-state mean-field interacting particle systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 85-125
- Print publication:
- March 2023
-
- Article
- Export citation
Limit laws for large
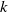 $k$th-nearest neighbor balls
$k$th-nearest neighbor balls
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 July 2022, pp. 880-894
- Print publication:
- September 2022
-
- Article
-
- You have access
- HTML
- Export citation
Limit theorems for random points in a simplex
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 June 2022, pp. 685-701
- Print publication:
- September 2022
-
- Article
- Export citation
Central limit theorem for bifurcating markov chains under L2-ergodic conditions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 999-1031
- Print publication:
- December 2022
-
- Article
- Export citation
Measuring reciprocity in a directed preferential attachment network
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 718-742
- Print publication:
- September 2022
-
- Article
- Export citation
Sub-tree counts on hyperbolic random geometric graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 1032-1069
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
A Dynamic Taylor’s law
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 24 June 2022, pp. 584-607
- Print publication:
- June 2022
-
- Article
- Export citation
Limit theorems for continuous-state branching processes with immigration
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 599-624
- Print publication:
- June 2022
-
- Article
- Export citation
Normal Approximation for Functions of Hidden Markov Models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 536-569
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
The critical mean-field Chayes–Machta dynamics
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 11 May 2022, pp. 924-975
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distribution of tree parameters by martingale approach
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 29 April 2022, pp. 737-764
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local limit theorems in relatively hyperbolic groups II: the non-spectrally degenerate case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 764-830
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On large-deviation probabilities for the empirical distribution of branching random walks with heavy tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 24 March 2022, pp. 471-494
- Print publication:
- June 2022
-
- Article
- Export citation
Limit theorems for critical branching processes in a finite-state-space Markovian environment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 01 March 2022, pp. 111-140
- Print publication:
- March 2022
-
- Article
- Export citation
Sums of random multiplicative functions over function fields with few irreducible factors
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 715-726
- Print publication:
- November 2022
-
- Article
- Export citation
Limit theorems and structural properties of the cat-and-mouse Markov chain and its generalisations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 141-166
- Print publication:
- March 2022
-
- Article
- Export citation