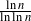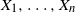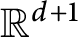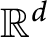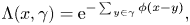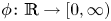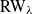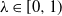Refine listing
Actions for selected content:
1047 results in 60Fxx
Strong convergence of infinite color balanced urns under uniform ergodicity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 853-865
- Print publication:
- September 2020
-
- Article
- Export citation
Trees grown under young-age preferential attachment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 911-927
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
Functional central limit theorems and moderate deviations for Poisson cluster processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 916-941
- Print publication:
- September 2020
-
- Article
- Export citation
Oscillations for order statistics of some discrete processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 703-719
- Print publication:
- September 2020
-
- Article
- Export citation
On moderate deviations in Poisson approximation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 1005-1027
- Print publication:
- September 2020
-
- Article
- Export citation
Renewal in Hawkes processes with self-excitation and inhibition
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 879-915
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
Breaking bivariate records
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 18 August 2020, pp. 105-123
-
- Article
- Export citation
A new approach to weak convergence of random cones and polytopes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 11 August 2020, pp. 1627-1647
- Print publication:
- December 2021
-
- Article
- Export citation
On a class of random walks in simplexes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 409-428
- Print publication:
- June 2020
-
- Article
- Export citation
Finite-time ruin probabilities under large-claim reinsurance treaties for heavy-tailed claim sizes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 513-530
- Print publication:
- June 2020
-
- Article
- Export citation
Central limit theorems for nearly long range dependent subordinated linear processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 637-656
- Print publication:
- June 2020
-
- Article
- Export citation
Tertiles and the time constant
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 407-408
- Print publication:
- June 2020
-
- Article
- Export citation
Limit theory for unbiased and consistent estimators of statistics of random tessellations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 679-702
- Print publication:
- June 2020
-
- Article
- Export citation
Small-Time smile for the multifactor volatility heston model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1070-1087
- Print publication:
- December 2020
-
- Article
- Export citation
Limit theorems for sequential MCMC methods
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 377-403
- Print publication:
- June 2020
-
- Article
- Export citation
Limit theorems for additive functionals of continuous time random walks
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 28 May 2020, pp. 799-820
- Print publication:
- April 2021
-
- Article
- Export citation
The size of the primes obstructing the existence of rational points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 652-704
- Print publication:
- April 2021
-
- Article
- Export citation
A non-exponential extension of Sanov’s theorem via convex duality
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 61-101
- Print publication:
- March 2020
-
- Article
- Export citation
An invariance principle and a large deviation principle for the biased random walk on
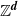 ${\mathbb{Z}}^{\lowercase{\textbf{\textit{d}}}}$
${\mathbb{Z}}^{\lowercase{\textbf{\textit{d}}}}$
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 295-313
- Print publication:
- March 2020
-
- Article
- Export citation
Uniform asymptotic normality of weighted sums of short-memory linear processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 174-195
- Print publication:
- March 2020
-
- Article
- Export citation