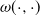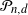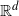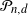Refine listing
Actions for selected content:
1827 results in 60Gxx
ON STATISTICAL PROPERTIES OF NONLINEAR FUNCTIONALS OF RANDOM FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 18 September 2020, pp. 338-340
- Print publication:
- April 2021
-
- Article
-
- You have access
- Export citation
Existence of Gibbs point processes with stable infinite range interaction
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 775-791
- Print publication:
- September 2020
-
- Article
- Export citation
Almost sure central limit theorems in stochastic geometry
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 705-734
- Print publication:
- September 2020
-
- Article
- Export citation
On branching models with alarm triggerings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 734-759
- Print publication:
- September 2020
-
- Article
- Export citation
Decorrelation of a class of Gibbs particle processes and asymptotic properties of U-statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 928-955
- Print publication:
- September 2020
-
- Article
- Export citation
Strong convergence of infinite color balanced urns under uniform ergodicity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 853-865
- Print publication:
- September 2020
-
- Article
- Export citation
Ergodicity of affine processes on the cone of symmetric positive semidefinite matrices
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 825-854
- Print publication:
- September 2020
-
- Article
- Export citation
Functional central limit theorems and moderate deviations for Poisson cluster processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 916-941
- Print publication:
- September 2020
-
- Article
- Export citation
Oscillations for order statistics of some discrete processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 703-719
- Print publication:
- September 2020
-
- Article
- Export citation
Renewal in Hawkes processes with self-excitation and inhibition
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 879-915
- Print publication:
- September 2020
-
- Article
- Export citation
Mean square rate of convergence for random walk approximation of forward-backward SDEs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 735-771
- Print publication:
- September 2020
-
- Article
- Export citation
Randomised rules for stopping problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 981-1004
- Print publication:
- September 2020
-
- Article
- Export citation
Breaking bivariate records
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 18 August 2020, pp. 105-123
-
- Article
- Export citation
SECOND ORDER SUBEXPONENTIALITY AND INFINITE DIVISIBILITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 22 June 2020, pp. 367-390
- Print publication:
- June 2022
-
- Article
- Export citation
On Pisier’s inequality for UMD targets
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 15 June 2020, pp. 282-291
- Print publication:
- June 2021
-
- Article
- Export citation
Simultaneous ruin probability for two-dimensional brownian risk model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 597-612
- Print publication:
- June 2020
-
- Article
- Export citation
Central limit theorems for nearly long range dependent subordinated linear processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 637-656
- Print publication:
- June 2020
-
- Article
- Export citation
The equilibrium states of large networks of Erlang queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 617-654
- Print publication:
- June 2020
-
- Article
- Export citation
Fluctuation identities for Omega-killed spectrally negative Markov additive processes and dividend problem
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 404-432
- Print publication:
- June 2020
-
- Article
- Export citation
Absorption probabilities for Gaussian polytopes and regular spherical simplices
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 588-616
- Print publication:
- June 2020
-
- Article
- Export citation