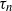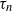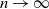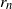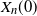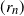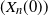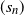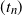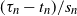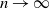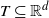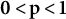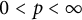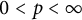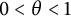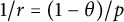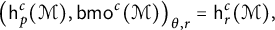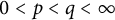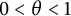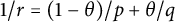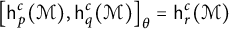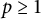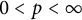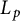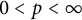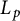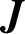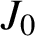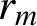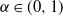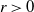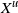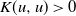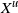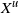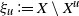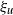Refine listing
Actions for selected content:
1838 results in 60Gxx
The Fokker–Planck equation for the time-changed fractional Ornstein–Uhlenbeck stochastic process
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 21 September 2021, pp. 1032-1057
- Print publication:
- August 2022
-
- Article
- Export citation
Non-Gaussian fluctuations of randomly trapped random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 801-838
- Print publication:
- September 2021
-
- Article
- Export citation
Pathwise large deviations for the rough Bergomi model: Corrigendum
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 849-850
- Print publication:
- September 2021
-
- Article
-
- You have access
- HTML
- Export citation
Estimating tails of independently stopped random walks using concave approximations of hazard functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 773-793
- Print publication:
- September 2021
-
- Article
- Export citation
Extinction time of the logistic process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 637-676
- Print publication:
- September 2021
-
- Article
- Export citation
Diffusion approximation of multi-class Hawkes processes: Theoretical and numerical analysis
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 716-756
- Print publication:
- September 2021
-
- Article
- Export citation
Long range dependence of heavy-tailed random functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 569-593
- Print publication:
- September 2021
-
- Article
- Export citation
A transient Cramér–Lundberg model with applications to credit risk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 721-745
- Print publication:
- September 2021
-
- Article
- Export citation
Rejection- and importance-sampling-based perfect simulation for Gibbs hard-sphere models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 839-885
- Print publication:
- September 2021
-
- Article
- Export citation
Variations of the elephant random walk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 805-829
- Print publication:
- September 2021
-
- Article
- Export citation
Interpolation between noncommutative martingale Hardy and BMO spaces: the case
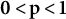 $\textbf {0<p<1}$
$\textbf {0<p<1}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 25 August 2021, pp. 1700-1744
- Print publication:
- December 2022
-
- Article
- Export citation
OPTION PRICING UNDER THE FRACTIONAL STOCHASTIC VOLATILITY MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 123-142
-
- Article
- Export citation
Mixing rates for potentials of non-summable variations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 2823-2840
- Print publication:
- September 2022
-
- Article
- Export citation
ON AN INTEGRAL OF
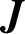 $\boldsymbol {J}$-BESSEL FUNCTIONS AND ITS APPLICATION TO MAHLER MEASURE
$\boldsymbol {J}$-BESSEL FUNCTIONS AND ITS APPLICATION TO MAHLER MEASURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 09 July 2021, pp. 223-235
- Print publication:
- April 2022
-
- Article
- Export citation
Continuum line-of-sight percolation on Poisson–Voronoi tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 510-536
- Print publication:
- June 2021
-
- Article
- Export citation
A generalised Dickman distribution and the number of species in a negative binomial process model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 370-399
- Print publication:
- June 2021
-
- Article
- Export citation
Exact simulation of Ornstein–Uhlenbeck tempered stable processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 347-371
- Print publication:
- June 2021
-
- Article
- Export citation
Population dynamics driven by truncated stable processes with Markovian switching
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 505-522
- Print publication:
- June 2021
-
- Article
- Export citation
A class of solvable multidimensional stopping problems in the presence of Knightian uncertainty
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 400-424
- Print publication:
- June 2021
-
- Article
- Export citation
Couplings for determinantal point processes and their reduced Palm distributions with a view to quantifying repulsiveness
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 469-483
- Print publication:
- June 2021
-
- Article
- Export citation