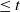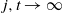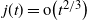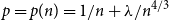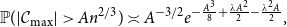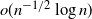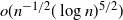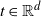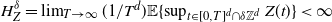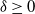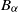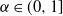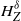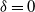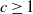Refine listing
Actions for selected content:
1838 results in 60Gxx
Sums of random multiplicative functions over function fields with few irreducible factors
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 715-726
- Print publication:
- November 2022
-
- Article
- Export citation
Kingman’s model with random mutation probabilities: convergence and condensation I
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 25 February 2022, pp. 311-335
- Print publication:
- March 2022
-
- Article
- Export citation
STATIONARY MARKOVIAN ARRIVAL PROCESSES: RESULTS AND OPEN PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 22 February 2022, pp. 54-68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Renewal theory for iterated perturbed random walks on a general branching process tree: intermediate generations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 421-446
- Print publication:
- June 2022
-
- Article
- Export citation
Exact simulation of extrinsic stress-release processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 14 February 2022, pp. 105-117
- Print publication:
- March 2022
-
- Article
- Export citation
Unusually large components in near-critical Erdős–Rényi graphs via ballot theorems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 840-869
-
- Article
- Export citation
Efficient conditional Monte Carlo simulations for the exponential integrals of Gaussian random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 366-383
- Print publication:
- June 2022
-
- Article
- Export citation
Log-concavity and other concepts of bivariate increasing failure rate distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 325-337
- Print publication:
- June 2022
-
- Article
- Export citation
Large-deviation results for triangular arrays of semiexponential random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 399-420
- Print publication:
- June 2022
-
- Article
- Export citation
A stochastic process on a network with connections to Laplacian systems of equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 21 January 2022, pp. 254-278
- Print publication:
- March 2022
-
- Article
- Export citation
Rate of strong convergence to Markov-modulated Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 1-16
- Print publication:
- March 2022
-
- Article
- Export citation
On the continuity of Pickands constants
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 187-201
- Print publication:
- March 2022
-
- Article
- Export citation
Replica-mean-field limits of fragmentation-interaction-aggregation processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 38-59
- Print publication:
- March 2022
-
- Article
- Export citation
Fragmentations with self-similar branching speeds
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1149-1189
- Print publication:
- December 2021
-
- Article
- Export citation
General drawdown of general tax model in a time-homogeneous Markov framework
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1131-1151
- Print publication:
- December 2021
-
- Article
- Export citation
Necessity of weak subordination for some strongly subordinated Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 868-879
- Print publication:
- December 2021
-
- Article
- Export citation
On the finiteness and tails of perpetuities under a Lamperti–Kiu MAP
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1086-1113
- Print publication:
- December 2021
-
- Article
- Export citation
Sparse regular variation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1115-1148
- Print publication:
- December 2021
-
- Article
- Export citation
Two poisson limit theorems for the coupon collector’s problem with group drawings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 966-977
- Print publication:
- December 2021
-
- Article
- Export citation
Shot noise processes with randomly delayed cluster arrivals and dependent noises in the large-intensity regime
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1190-1221
- Print publication:
- December 2021
-
- Article
- Export citation