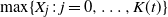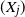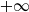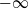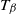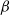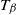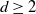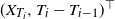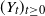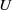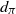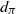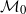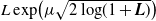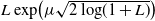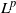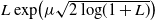Refine listing
Actions for selected content:
1838 results in 60Gxx
On extremes of random clusters and marked renewal cluster processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 367-381
- Print publication:
- June 2023
-
- Article
- Export citation
On the splitting and aggregating of Hawkes processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 676-692
- Print publication:
- June 2023
-
- Article
- Export citation
Exponential ergodicity for a class of Markov processes with interactions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 465-478
- Print publication:
- June 2023
-
- Article
- Export citation
The fundamental inequality for cocompact Fuchsian groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 November 2022, e102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On moments of downward passage times for spectrally negative Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 16 November 2022, pp. 452-464
- Print publication:
- June 2023
-
- Article
- Export citation
A decomposition for Lévy processes inspected at Poisson moments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 557-569
- Print publication:
- June 2023
-
- Article
- Export citation
An elementary approach to component sizes in critical random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 11 November 2022, pp. 1228-1242
- Print publication:
- December 2022
-
- Article
- Export citation
Asymptotic behavior and quasi-limiting distributions on time-fractional birth and death processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 11 November 2022, pp. 1199-1227
- Print publication:
- December 2022
-
- Article
- Export citation
A growth-fragmentation model connected to the ricocheted stable process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 November 2022, pp. 493-503
- Print publication:
- June 2023
-
- Article
- Export citation
Bose–Einstein condensation for particles with repulsive short-range pair interactions in a Poisson random external potential in
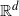 $\mathbb{R}^{d}$
$\mathbb{R}^{d}$
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 28 October 2022, pp. 382-393
- Print publication:
- June 2023
-
- Article
- Export citation
A note related to the CS decomposition and the BK inequality for discrete determinantal processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 24 October 2022, pp. 189-203
- Print publication:
- March 2023
-
- Article
- Export citation
Inheritance of strong mixing and weak dependence under renewal sampling
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 14 October 2022, pp. 435-451
- Print publication:
- June 2023
-
- Article
- Export citation
Large deviations of Poisson Telecom processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 12 October 2022, pp. 267-283
- Print publication:
- March 2023
-
- Article
- Export citation
Multivariate Poisson and Poisson process approximations with applications to Bernoulli sums and
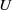 $U$-statistics
$U$-statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 30 September 2022, pp. 223-240
- Print publication:
- March 2023
-
- Article
-
- You have access
- HTML
- Export citation
CONVERGENCE RATE FOR STATISTICS OF POINT PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 28 September 2022, pp. 511-512
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
From reflected Lévy processes to stochastically monotone Markov processes via generalized inverses and supermodularity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 68-84
- Print publication:
- March 2023
-
- Article
- Export citation
Limit theory for U-statistics under geometric and topological constraints with rare events
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 14 September 2022, pp. 314-340
- Print publication:
- March 2023
-
- Article
- Export citation
Optimal stopping under g-Expectation with
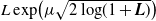 ${L}\exp\bigl(\mu\sqrt{2\log\!(1+\textbf{L})}\bigr)$-integrable reward process
${L}\exp\bigl(\mu\sqrt{2\log\!(1+\textbf{L})}\bigr)$-integrable reward process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 14 September 2022, pp. 241-252
- Print publication:
- March 2023
-
- Article
- Export citation
Critical cluster cascades
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 13 September 2022, pp. 357-381
- Print publication:
- June 2023
-
- Article
- Export citation
Optimal multiple stopping problem under nonlinear expectation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 151-178
- Print publication:
- March 2023
-
- Article
- Export citation