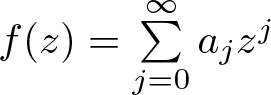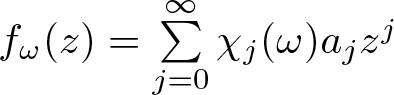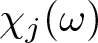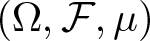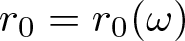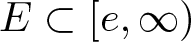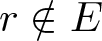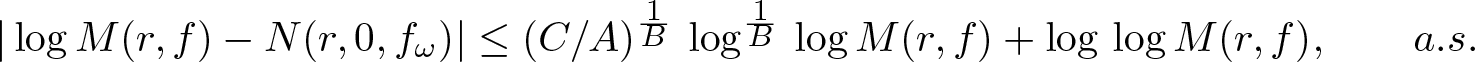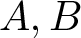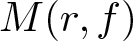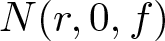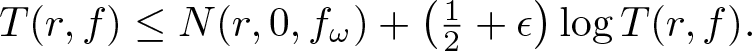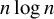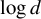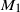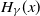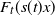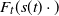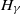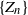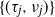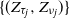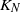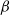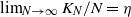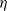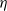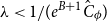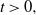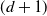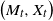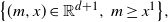Refine listing
Actions for selected content:
1838 results in 60Gxx
An inaccuracy measure between non-explosive point processes with applications to Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 25 October 2023, pp. 735-756
- Print publication:
- June 2024
-
- Article
- Export citation
Inequalities concerning maximum modulus and zeros of random entire functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 19 October 2023, pp. 57-78
-
- Article
- Export citation
Central limit theorem in complete feedback games
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 16 October 2023, pp. 654-666
- Print publication:
- June 2024
-
- Article
- Export citation
Stochastic ordering results on the duration of the gambler’s ruin game
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 603-621
- Print publication:
- June 2024
-
- Article
- Export citation
Optimal stopping methodology for the secretary problem with random queries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 578-602
- Print publication:
- June 2024
-
- Article
- Export citation
Collapse and diffusion in harmonic activation and transport
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 September 2023, e85
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fluctuations of the local times of the self-repelling random walk with directed edges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 September 2023, pp. 545-586
- Print publication:
- June 2024
-
- Article
- Export citation
Adaptation of a population to a changing environment in the light of quasi-stationarity
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 30 August 2023, pp. 235-286
- Print publication:
- March 2024
-
- Article
- Export citation
Strong convergence of peaks over a threshold
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 23 August 2023, pp. 529-539
- Print publication:
- June 2024
-
- Article
- Export citation
Branching processes in random environments with thresholds
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 495-544
- Print publication:
- June 2024
-
- Article
- Export citation
Migration–contagion processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 18 August 2023, pp. 71-105
- Print publication:
- March 2024
-
- Article
- Export citation
Toeplitz determinants with a one-cut regular potential and Fisher–Hartwig singularities I. Equilibrium measure supported on the unit circle
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 1431-1472
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reliability analyses of linear two-dimensional consecutive k-type systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 14 August 2023, pp. 439-464
- Print publication:
- June 2024
-
- Article
- Export citation
Quasipolynomial-time algorithms for Gibbs point processes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 11 August 2023, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stopping problems with an unknown state
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 09 August 2023, pp. 515-528
- Print publication:
- June 2024
-
- Article
- Export citation
Heavy-traffic limits for parallel single-server queues with randomly split Hawkes arrival processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 07 August 2023, pp. 490-514
- Print publication:
- June 2024
-
- Article
- Export citation
SCHEDULING IN QUEUEING SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 27 July 2023, pp. 349-350
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
Weak random periodic solutions of random dynamical systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 12 July 2023, pp. 137-151
- Print publication:
- March 2024
-
- Article
- Export citation
PDE for the joint law of the pair of a continuous diffusion and its running maximum
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1171-1210
- Print publication:
- December 2023
-
- Article
- Export citation
Expanding measures: Random walks and rigidity on homogeneous spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 July 2023, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation