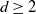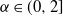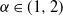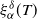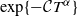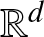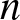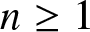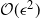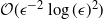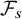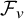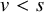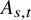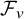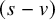Refine listing
Actions for selected content:
1838 results in 60Gxx
On the strong stability of ergodic iterations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 05 November 2024, pp. 284-297
- Print publication:
- March 2025
-
- Article
- Export citation
The impact of pinning points on memorylessness in Lévy random bridges
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 15 October 2024, pp. 172-187
- Print publication:
- March 2025
-
- Article
- Export citation
Sampling repulsive Gibbs point processes using random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 63-89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On transience of
 $\mathrm{M}/\mathrm{G}/\infty$ queues
$\mathrm{M}/\mathrm{G}/\infty$ queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 572-575
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transience of continuous-time conservative random walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 153-171
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A non-homogeneous alternating renewal process model for interval censoring
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 16 September 2024, pp. 494-515
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-hyperuniformity of Gibbs point processes with short-range interactions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 August 2024, pp. 1380-1406
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the speed of convergence of discrete Pickands constants to continuous ones
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 31 July 2024, pp. 111-135
- Print publication:
- March 2025
-
- Article
- Export citation
Tail asymptotics and precise large deviations for some Poisson cluster processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 26 July 2024, pp. 204-240
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Change of measure in a Heston–Hawkes stochastic volatility model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 24 July 2024, pp. 1370-1399
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the probability of a Pareto record
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 04 June 2024, pp. 752-764
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Persistence of spectral projections for stochastic operators on large tensor products
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-14
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bivariate tempered space-fractional Poisson process and shock models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 23 May 2024, pp. 1485-1501
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Co-spectral radius for countable equivalence relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 3385-3427
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A remark on exact simulation of tempered stable Ornstein–Uhlenbeck processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1196-1198
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Inhomogeneous Poisson processes in the disk and interpolation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 30 April 2024, pp. 749-777
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Antithetic multilevel particle filters
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1400-1439
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An extension of the stochastic sewing lemma and applications to fractional stochastic calculus
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 April 2024, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An extreme worst-case risk measure by expectile
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1195-1214
- Print publication:
- December 2024
-
- Article
- Export citation
Topological reconstruction of compact supports of dependent stationary random variables
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1339-1369
- Print publication:
- December 2024
-
- Article
- Export citation