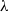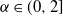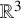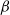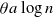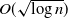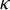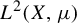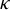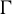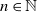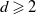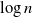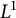Refine listing
Actions for selected content:
1838 results in 60Gxx
An elementary approach to the inverse first-passage-time problem for soft-killed Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 July 2023, pp. 279-300
- Print publication:
- March 2024
-
- Article
- Export citation
Optimal coupling of jumpy Brownian motion on the circle
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 July 2023, pp. 18-32
- Print publication:
- March 2024
-
- Article
- Export citation
Normal approximation in total variation for statistics in geometric probability
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 03 July 2023, pp. 106-155
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
 $\alpha$-Stable convergence of heavy-/light-tailed infinitely wide neural networks
$\alpha$-Stable convergence of heavy-/light-tailed infinitely wide neural networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 03 July 2023, pp. 1415-1441
- Print publication:
- December 2023
-
- Article
- Export citation
A Monte Carlo algorithm for the extrema of tempered stable processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 30 June 2023, pp. 1362-1389
- Print publication:
- December 2023
-
- Article
- Export citation
OPTIMAL STOPPING PROBLEMS WITH A RANDOM TIME HORIZON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 345-346
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
Beltrami fields exhibit knots and chaos almost surely
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 June 2023, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONDITIONS FOR RECURRENCE AND TRANSIENCE FOR TIME-INHOMOGENEOUS BIRTH-AND-DEATH PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 393-402
- Print publication:
- April 2024
-
- Article
- Export citation
Continuous-time locally stationary time series models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 20 June 2023, pp. 965-998
- Print publication:
- September 2023
-
- Article
- Export citation
Monotonicity of implied volatility for perpetual put options
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 19 June 2023, pp. 301-310
- Print publication:
- March 2024
-
- Article
- Export citation
On sparsity, power-law, and clustering properties of graphex processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 1211-1253
- Print publication:
- December 2023
-
- Article
- Export citation
No arbitrage and multiplicative special semimartingales
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 09 June 2023, pp. 1033-1074
- Print publication:
- September 2023
-
- Article
- Export citation
Upper large deviations for power-weighted edge lengths in spatial random networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 34-70
- Print publication:
- March 2024
-
- Article
- Export citation
Moderate deviations inequalities for Gaussian process regression
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 172-197
- Print publication:
- March 2024
-
- Article
- Export citation
Bootstrap percolation in random geometric graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 31 May 2023, pp. 1254-1300
- Print publication:
- December 2023
-
- Article
- Export citation
On the spectral theory of groups of automorphisms of S-adic nilmanifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 705-726
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A branching random walk in the presence of a hard wall
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1-17
- Print publication:
- March 2024
-
- Article
- Export citation
Kalikow decomposition for counting processes with stochastic intensity and application to simulation algorithms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 19 May 2023, pp. 1469-1500
- Print publication:
- December 2023
-
- Article
- Export citation
Strong Shannon–McMillan–Breiman’s theorem for locally compact groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 05 May 2023, pp. 1274-1279
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mixing time bounds for edge flipping on regular graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 1317-1332
- Print publication:
- December 2023
-
- Article
- Export citation