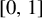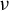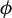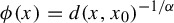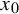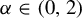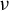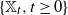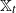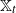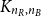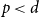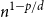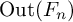Refine listing
Actions for selected content:
1838 results in 60Gxx
Constrained optimal stopping under a regime-switching model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 27 March 2024, pp. 1220-1239
- Print publication:
- December 2024
-
- Article
- Export citation
Multidimensional random motions with a natural number of finite velocities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 March 2024, pp. 1033-1063
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalised shot-noise representations of stochastic systems driven by non-Gaussian Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1215-1250
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inequalities between time and customer averages for HNB(W)UE arrival processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1199-1219
- Print publication:
- December 2024
-
- Article
- Export citation
Discounted densities of overshoot and undershoot for Lévy processes with applications in finance
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 19 March 2024, pp. 644-667
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic results for sums and extremes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 13 March 2024, pp. 1153-1171
- Print publication:
- December 2024
-
- Article
- Export citation
Connectivity of random graphs after centrality-based vertex removal
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 23 February 2024, pp. 967-998
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable laws for random dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 14 February 2024, pp. 3041-3090
- Print publication:
- November 2024
-
- Article
- Export citation
Scaling limit of the local time of random walks conditioned to stay positive
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 13 February 2024, pp. 1060-1074
- Print publication:
- September 2024
-
- Article
- Export citation
Central limit theorem for a birth–growth model with poisson arrivals and random growth speed
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1004-1032
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A queueing system with an SIR-type infection
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 16 January 2024, pp. 559-578
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APPROXIMATE PRICING OF DERIVATIVES UNDER FRACTIONAL STOCHASTIC VOLATILITY MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 15 January 2024, pp. 229-247
-
- Article
- Export citation
Max-linear graphical models with heavy-tailed factors on trees of transitive tournaments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 621-665
- Print publication:
- June 2024
-
- Article
- Export citation
Shock models governed by an inverse gamma mixed Poisson process
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 459-480
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak convergence of the extremes of branching Lévy processes with regularly varying tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 December 2023, pp. 622-643
- Print publication:
- June 2024
-
- Article
- Export citation
Speed of extinction for continuous-state branching processes in a weakly subcritical Lévy environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 886-908
- Print publication:
- September 2024
-
- Article
- Export citation
On minimum spanning trees for random Euclidean bipartite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 319-350
-
- Article
- Export citation
Characteristics of the switch process and geometric divisibility
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 802-809
- Print publication:
- September 2024
-
- Article
- Export citation
LINEAR GROWTH OF TRANSLATION LENGTHS OF RANDOM ISOMETRIES ON GROMOV HYPERBOLIC SPACES AND TEICHMÜLLER SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1751-1795
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a time-changed variant of the generalized counting process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 716-738
- Print publication:
- June 2024
-
- Article
- Export citation