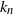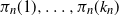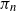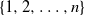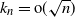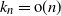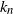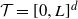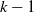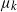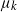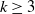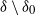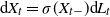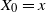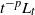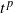Refine listing
Actions for selected content:
1838 results in 60Gxx
Lower bound for the expected supremum of fractional brownian motion using coupling
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1232-1248
- Print publication:
- December 2023
-
- Article
- Export citation
Characterization theorems for pseudo cross-variograms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1219-1231
- Print publication:
- December 2023
-
- Article
- Export citation
Asymptotic behaviour of the first positions of uniform parking functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 1201-1218
- Print publication:
- December 2023
-
- Article
- Export citation
A spatial mutation model with increasing mutation rates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 1157-1180
- Print publication:
- December 2023
-
- Article
- Export citation
Workload analysis of a two-queue fluid polling model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 March 2023, pp. 1003-1030
- Print publication:
- September 2023
-
- Article
- Export citation
Sandwiched SDEs with unbounded drift driven by Hölder noises
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 08 March 2023, pp. 927-964
- Print publication:
- September 2023
-
- Article
- Export citation
On the cumulant transforms for Hawkes processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 23 February 2023, pp. 528-541
- Print publication:
- June 2023
-
- Article
- Export citation
Optimal proportional reinsurance to maximize an insurer’s exponential utility under unobservable drift
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 21 February 2023, pp. 874-894
- Print publication:
- September 2023
-
- Article
- Export citation
Sojourn functionals for spatiotemporal Gaussian random fields with long memory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 09 February 2023, pp. 148-165
- Print publication:
- March 2023
-
- Article
- Export citation
A dual risk model with additive and proportional gains: ruin probability and dividends
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 February 2023, pp. 549-580
- Print publication:
- June 2023
-
- Article
- Export citation
On impact of largest claims reinsurance treaties on the ceding company’s loss reserve
- Part of
-
- Journal:
- Annals of Actuarial Science / Volume 17 / Issue 2 / July 2023
- Published online by Cambridge University Press:
- 01 February 2023, pp. 328-357
-
- Article
- Export citation
Reciprocal properties of random fields on undirected graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 781-796
- Print publication:
- September 2023
-
- Article
- Export citation
Multiple-drawing dynamic Friedman urns with opposite-reinforcement
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 26 January 2023, pp. 115-129
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Predicting the last zero before an exponential time of a spectrally negative Lévy process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 611-642
- Print publication:
- June 2023
-
- Article
- Export citation
FAST METHODS FOR FITTING LOG-GAUSSIAN COX PROCESS MODELS IN ECOLOGY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 344-345
- Print publication:
- April 2023
-
- Article
-
- You have access
- HTML
- Export citation
Short-time behavior of solutions to Lévy-driven stochastic differential equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 765-780
- Print publication:
- September 2023
-
- Article
- Export citation
Invariant Galton–Watson trees: metric properties and attraction with respect to generalized dynamical pruning
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 643-671
- Print publication:
- June 2023
-
- Article
- Export citation
With or without replacement? Sampling uncertainty in Shepp’s urn scheme
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 22 December 2022, pp. 661-675
- Print publication:
- June 2023
-
- Article
- Export citation
A factor of i.i.d. with uniform marginals and infinite clusters spanned by equal labels
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 22 December 2022, pp. 3707-3725
- Print publication:
- November 2023
-
- Article
- Export citation
Reflection principle for finite-velocity random motions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 479-492
- Print publication:
- June 2023
-
- Article
- Export citation