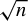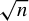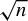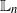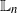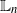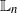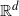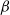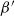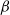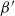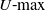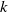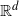Refine listing
Actions for selected content:
1838 results in 60Gxx
Rational points on nonlinear horocycles and pigeonhole statistics for the fractional parts of
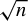 $\sqrt {n}$
$\sqrt {n}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 3108-3130
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ASYMPTOTIC PROPERTIES OF NONLINEAR FUNCTIONALS OF RANDOM FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 05 September 2022, pp. 518-521
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
Renewal theory for iterated perturbed random walks on a general branching process tree: Early generations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 45-67
- Print publication:
- March 2023
-
- Article
- Export citation
Log-normalization constant estimation using the ensemble Kalman–Bucy filter with application to high-dimensional models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 September 2022, pp. 1139-1163
- Print publication:
- December 2022
-
- Article
- Export citation
On q-scale functions of spectrally negative Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 56-84
- Print publication:
- March 2023
-
- Article
- Export citation
On the ruin probability of a generalized Cramér–Lundberg model driven by mixed Poisson processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 12 September 2022, pp. 849-859
- Print publication:
- September 2022
-
- Article
- Export citation
STOCHASTIC PROCESSES WITH APPLICATIONS IN PHYSICS AND INSURANCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 30 August 2022, pp. 513-517
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
Unified approach for solving exit problems for additive-increase and multiplicative-decrease processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 30 August 2022, pp. 85-105
- Print publication:
- March 2023
-
- Article
- Export citation
The direct-connectedness function in the random connection model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 24 August 2022, pp. 179-222
- Print publication:
- March 2023
-
- Article
- Export citation
ON MULTIFRACTIONALITY OF SPHERICAL RANDOM FIELDS WITH COSMOLOGICAL APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 18 August 2022, pp. 90-118
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A deep look into the dagum family of isotropic covariance functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 August 2022, pp. 1026-1041
- Print publication:
- December 2022
-
- Article
- Export citation
On strongly rigid hyperfluctuating random measures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 August 2022, pp. 948-961
- Print publication:
- December 2022
-
- Article
- Export citation
Characterization of random variables with stationary digits
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 August 2022, pp. 931-947
- Print publication:
- December 2022
-
- Article
- Export citation
The
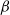 $\beta$-Delaunay tessellation: Description of the model and geometry of typical cells
$\beta$-Delaunay tessellation: Description of the model and geometry of typical cells
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 01 August 2022, pp. 1252-1290
- Print publication:
- December 2022
-
- Article
- Export citation
The hit-and-run version of top-to-random
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 12 July 2022, pp. 860-879
- Print publication:
- September 2022
-
- Article
- Export citation
Generalized limit theorems for U-max statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 825-848
- Print publication:
- September 2022
-
- Article
- Export citation
An extended class of univariate and multivariate generalized Pólya processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 974-997
- Print publication:
- September 2022
-
- Article
- Export citation
Limit laws for large
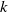 $k$th-nearest neighbor balls
$k$th-nearest neighbor balls
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 July 2022, pp. 880-894
- Print publication:
- September 2022
-
- Article
-
- You have access
- HTML
- Export citation
Hitting times for second-order random walks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 04 July 2022, pp. 642-666
-
- Article
- Export citation
Discounted optimal stopping problems in first-passage time models with random thresholds
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 27 June 2022, pp. 714-733
- Print publication:
- September 2022
-
- Article
- Export citation