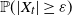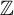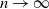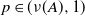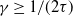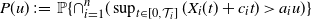Refine listing
Actions for selected content:
1838 results in 60Gxx
Non-asymptotic control of the cumulative distribution function of Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 913-944
- Print publication:
- September 2022
-
- Article
- Export citation
Measuring reciprocity in a directed preferential attachment network
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 718-742
- Print publication:
- September 2022
-
- Article
- Export citation
Moments of Markovian growth–collapse processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1070-1093
- Print publication:
- December 2022
-
- Article
- Export citation
BERNOULLI ACTIONS OF TYPE III
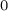 $_0$ WITH PRESCRIBED ASSOCIATED FLOW
$_0$ WITH PRESCRIBED ASSOCIATED FLOW
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 14 June 2022, pp. 71-122
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probability of total domination for transient reflecting processes in a quadrant
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1094-1138
- Print publication:
- December 2022
-
- Article
- Export citation
STOCHASTIC MODELLING AND STATISTICAL ANALYSIS OF SPATIAL AND LONG-RANGE DEPENDENT DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 170-173
- Print publication:
- August 2022
-
- Article
-
- You have access
- HTML
- Export citation
Unified signature cumulants and generalized Magnus expansions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Dynamic Taylor’s law
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 24 June 2022, pp. 584-607
- Print publication:
- June 2022
-
- Article
- Export citation
Discrete-time risk-aware optimal switching with non-adapted costs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 625-655
- Print publication:
- June 2022
-
- Article
- Export citation
Ruin probabilities with investments: smoothness, inegro-differential and ordinary differential equations, asymptotic behavior
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 24 June 2022, pp. 556-570
- Print publication:
- June 2022
-
- Article
- Export citation
On operator fractional Lévy motion: integral representations and time-reversibility
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 493-535
- Print publication:
- June 2022
-
- Article
- Export citation
Nash equilibrium structure of Cox process Hotelling games
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 570-598
- Print publication:
- June 2022
-
- Article
- Export citation
On the Sn/n problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 17 May 2022, pp. 571-583
- Print publication:
- June 2022
-
- Article
- Export citation
Optimal discounted drawdowns in a diffusion approximation under proportional reinsurance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 30 March 2022, pp. 527-540
- Print publication:
- June 2022
-
- Article
- Export citation
On large-deviation probabilities for the empirical distribution of branching random walks with heavy tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 24 March 2022, pp. 471-494
- Print publication:
- June 2022
-
- Article
- Export citation
An ephemerally self-exciting point process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 340-403
- Print publication:
- June 2022
-
- Article
- Export citation
Fair gambler’s ruin stochastically maximizes playing time
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 10 March 2022, pp. 656-659
- Print publication:
- June 2022
-
- Article
- Export citation
Probabilistic analysis of replicator–mutator equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 23 March 2022, pp. 167-201
- Print publication:
- March 2022
-
- Article
- Export citation
SINR percolation for Cox point processes with random powers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 23 March 2022, pp. 227-253
- Print publication:
- March 2022
-
- Article
- Export citation
Extrema of multi-dimensional Gaussian processes over random intervals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 81-104
- Print publication:
- March 2022
-
- Article
- Export citation