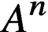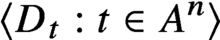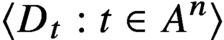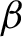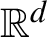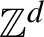Refine listing
Actions for selected content:
1827 results in 60Gxx
Tail asymptotics for the area under the excursion of a random walk with heavy-tailed increments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 217-237
- Print publication:
- March 2021
-
- Article
- Export citation
Self-exciting multifractional processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 22-41
- Print publication:
- March 2021
-
- Article
- Export citation
Double hypergeometric Lévy processes and self-similarity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 254-273
- Print publication:
- March 2021
-
- Article
- Export citation
A structure theorem for stochastic processes indexed by the discrete hypercube
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 28 January 2021, e8
-
- Article
-
- You have access
- Open access
- Export citation
Large deviations for a class of tempered subordinators and their inverse processes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 2030-2050
- Print publication:
- December 2021
-
- Article
- Export citation
Invariant densities for random systems of the interval
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 141-179
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Isomorphisms between determinantal point processes with translation-invariant kernels and Poisson point processes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 04 December 2020, pp. 3807-3820
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
A Bayesian sequential test for the drift of a fractional Brownian motion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1308-1324
- Print publication:
- December 2020
-
- Article
- Export citation
Asymptotic variance of Newton–Cotes quadratures based on randomized sampling points
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1284-1307
- Print publication:
- December 2020
-
- Article
- Export citation
Draw-down Parisian ruin for spectrally negative Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1164-1196
- Print publication:
- December 2020
-
- Article
- Export citation
A generalization of Matérn hard-core processes with applications to max-stable processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1298-1312
- Print publication:
- December 2020
-
- Article
- Export citation
A temporal factorization at the maximum for certain positive self-similar Markov processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1045-1069
- Print publication:
- December 2020
-
- Article
- Export citation
Generalised liouville processes and their properties
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1088-1110
- Print publication:
- December 2020
-
- Article
- Export citation
Synchronized Lévy queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1222-1233
- Print publication:
- December 2020
-
- Article
- Export citation
Exact sampling of determinantal point processes without eigendecomposition
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1198-1221
- Print publication:
- December 2020
-
- Article
- Export citation
Skeletal stochastic differential equations for superprocesses
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1111-1134
- Print publication:
- December 2020
-
- Article
- Export citation
Representations of hermite processes using local time of intersecting stationary stable regenerative sets
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1234-1251
- Print publication:
- December 2020
-
- Article
- Export citation
On Λ-Fleming–Viot processes with general frequency-dependent selection
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1162-1197
- Print publication:
- December 2020
-
- Article
- Export citation
Spread out random walks on homogeneous spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2020, pp. 3439-3473
- Print publication:
- November 2021
-
- Article
- Export citation
Markov chains with exponential return times are finitary
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 29 September 2020, pp. 2918-2926
- Print publication:
- October 2021
-
- Article
- Export citation