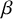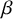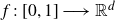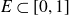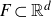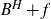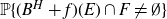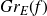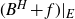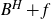Refine listing
Actions for selected content:
1838 results in 60Gxx
The bisexual branching processes affected by viral infectivity and with random control functions in random environments
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 21 January 2025, pp. 260-277
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The extremal landscape for the C
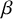 $\beta $E ensemble
$\beta $E ensemble
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 January 2025, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On stochastic control under poissonian intervention: optimality of a barrier strategy in a general Lévy model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 628-651
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fractional Brownian motion with deterministic drift: how critical is drift regularity in hitting probabilities
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 February 2025, pp. 103-132
- Print publication:
- January 2025
-
- Article
- Export citation
On affine multicolor urns grown under multiple drawing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 24 December 2024, pp. 808-831
- Print publication:
- June 2025
-
- Article
- Export citation
Rough multi-factor volatility for SPX and VIX options
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 16 December 2024, pp. 524-565
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal stopping of Gauss–Markov bridges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 04 December 2024, pp. 1-34
- Print publication:
- March 2025
-
- Article
- Export citation
Feller and ergodic properties of jump–move processes with applications to interacting particle systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 65-100
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the asymptotic normality of persistent Betti numbers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 492-523
- Print publication:
- June 2025
-
- Article
- Export citation
Discounted optimal stopping zero-sum games in diffusion type models with maxima and minima
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 241-270
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Brownian range and the Brownian reversal
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 775-794
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hidden tail chains and recurrence equations for dependence parameters associated with extremes of stationary higher-order Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 407-452
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence of the derivative martingale for the branching random walk in time-inhomogeneous random environment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 642-676
- Print publication:
- June 2025
-
- Article
- Export citation
Gaussian approximation and moderate deviations of Poisson shot noises with application to compound generalized Hawkes processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 305-345
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
First-passage time for Sinai’s random walk in a random environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 29 November 2024, pp. 756-774
- Print publication:
- June 2025
-
- Article
- Export citation
Widths of crossings in Poisson Boolean percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 603-627
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotics of the allele frequency spectrum and the number of alleles
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 516-540
- Print publication:
- June 2025
-
- Article
- Export citation
Random walks on groups and superlinear-divergent geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1403-1443
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hiring and firing – a signaling game
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 12 November 2024, pp. 697-711
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Expansion of the critical intensity for the random connection model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 08 November 2024, pp. 158-209
-
- Article
-
- You have access
- Open access
- HTML
- Export citation