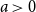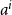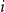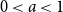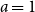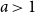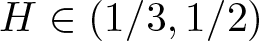Refine listing
Actions for selected content:
1838 results in 60Gxx
Exact solution to the Chow–Robbins game for almost all n, by using a catalan triangle
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 16 May 2025, pp. 1206-1241
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coupling results and Markovian structures for number representations of continuous random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1340-1359
- Print publication:
- December 2025
-
- Article
- Export citation
Exponentially preferential trees
- Part of
-
- Journal:
- Network Science / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 April 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Radially geometric stable distributions and processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 10 April 2025, pp. 1392-1429
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some conditional properties of superprocesses in random environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 08 April 2025, pp. 1156-1172
- Print publication:
- September 2025
-
- Article
- Export citation
Weighted maxima and sums of non-stationary random-length sequences in heavy-tailed models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1173-1192
- Print publication:
- September 2025
-
- Article
- Export citation
Approximation of the invariant measure for stable stochastic differential equations by the Euler–Maruyama scheme with decreasing step sizes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 31 March 2025, pp. 1000-1030
- Print publication:
- September 2025
-
- Article
- Export citation
Sample path moderate deviations for non-stationary power-law shot noise processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 28 March 2025, pp. 1105-1131
- Print publication:
- September 2025
-
- Article
- Export citation
Sufficientness postulates for measure-valued Pólya urn sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 28 March 2025, pp. 925-949
- Print publication:
- September 2025
-
- Article
- Export citation
Matrix representations of Wiener–Hopf factorisations for Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 05 March 2025, pp. 1028-1043
- Print publication:
- September 2025
-
- Article
- Export citation
Graph connectivity with fixed endpoints in the random-connection model
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 3 / July 2025
- Published online by Cambridge University Press:
- 21 February 2025, pp. 370-396
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reliability and optimal age replacement policy of a system subject to shocks following a Markovian arrival process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 14 February 2025, pp. 1010-1027
- Print publication:
- September 2025
-
- Article
- Export citation
EXPLORING OUT-OF-SAMPLE PREDICTION AND SPATIAL DEPENDENCY FOR COMPLEX BIG DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 380-382
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation
Extending Wormald’s differential equation method to one-sided bounds
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 06 February 2025, pp. 545-558
-
- Article
- Export citation
The spread of an epidemic: a game-theoretic approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 31 January 2025, pp. 749-810
- Print publication:
- September 2025
-
- Article
- Export citation
Large deviation principle for slow-fast rough differential equations via controlled rough paths
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 January 2025, pp. 1-31
-
- Article
- Export citation
QUENCHED CENTRAL LIMIT THEOREM FOR DVORETZKY COVERING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 28 January 2025, pp. 368-378
- Print publication:
- April 2025
-
- Article
- Export citation
Last exit time until first exit time for spectrally negative Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 24 January 2025, pp. 876-897
- Print publication:
- September 2025
-
- Article
- Export citation
Solution theory of fractional SDEs in complete subcritical regimes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal linear sofic approximations of countable groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 24 January 2025, pp. 245-268
- Print publication:
- May 2025
-
- Article
- Export citation