Refine listing
Actions for selected content:
1829 results in 60Gxx
Electronic Foreign-Exchange Markets and Passage Events of Independent Subordinators
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 138-152
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Fractional random fields associated with stochastic fractional heat equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 108-133
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
On the fundamental theorem of card counting, with application to the game of trente et quarante
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 90-107
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
A queue with semiperiodic traffic
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 160-184
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
The use of the variogram in construction of stationary time series models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1093-1103
- Print publication:
- December 2004
-
- Article
- Export citation
On a deposition process on the circle with disorder
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 996-1020
- Print publication:
- December 2004
-
- Article
- Export citation
Some fluctuation identities for Lévy processes with jumps of the same sign
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1191-1198
- Print publication:
- December 2004
-
- Article
- Export citation
The Kelly system maximizes median fortune
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1230-1236
- Print publication:
- December 2004
-
- Article
- Export citation
Filters and parameter estimation for a partially observable system subject to random failure with continuous-range observations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1212-1230
- Print publication:
- December 2004
-
- Article
- Export citation
Two-choice optimal stopping
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1116-1147
- Print publication:
- December 2004
-
- Article
- Export citation
The behavior of multivariate maxima of moving maxima processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1113-1123
- Print publication:
- December 2004
-
- Article
- Export citation
Overshoots over curved boundaries. II
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1148-1174
- Print publication:
- December 2004
-
- Article
- Export citation
Stopping the maximum of a correlated random walk, with cost for observation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 998-1007
- Print publication:
- December 2004
-
- Article
- Export citation
On the multifractal spectrum of the branching measure on a Galton–Watson tree
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1223-1229
- Print publication:
- December 2004
-
- Article
- Export citation
Random walks on a complete graph: a model for infection
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1008-1021
- Print publication:
- December 2004
-
- Article
- Export citation
Stochastic properties of the linear multifractional stable motion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1085-1115
- Print publication:
- December 2004
-
- Article
- Export citation
The mean comparison theorem cannot be extended to the Poisson case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1199-1202
- Print publication:
- December 2004
-
- Article
- Export citation
The first rendezvous time of Brownian motion and compound Poisson-type processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1059-1070
- Print publication:
- December 2004
-
- Article
- Export citation
Change-point models and conditionally pure birth processes: an inequality on the stochastic intensity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 939-952
- Print publication:
- December 2004
-
- Article
- Export citation
A continuous-time GARCH process driven by a Lévy process: stationarity and second-order behaviour
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 601-622
- Print publication:
- September 2004
-
- Article
- Export citation
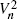 equal the expectation of the smaller of the two values chosen by the statistician when proceeding optimally. We obtain the asymptotic behaviour of the sequence
equal the expectation of the smaller of the two values chosen by the statistician when proceeding optimally. We obtain the asymptotic behaviour of the sequence 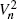 for a large class of
for a large class of 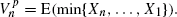 , as well as with the ‘prophet value’ sequence
, as well as with the ‘prophet value’ sequence 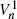
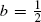 ), and for the
), and for the 