Refine listing
Actions for selected content:
1829 results in 60Gxx
The lifetime of a random set
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 566-580
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Weighted sums of subexponential random variables and their maxima
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 510-522
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Hidden regular variation and the rank transform
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 393-414
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Differentiation of some functionals of risk processes, and optimal reserve allocation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 379-392
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Fractional kinetic equations driven by Gaussian or infinitely divisible noise
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 366-392
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Multiperiod conditional distribution functions for conditionally normal GARCH(1, 1) models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 426-445
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Asymptotic expansions of convolutions of regularly varying distributions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 3 / June 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 339-371
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Geometrical characteristics of Gaussian sea waves
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 407-425
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Improving on bold play when the gambler is restricted
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 321-333
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Burgers' turbulence problem with linear or quadratic external potential
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 550-565
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Heterogeneous population dynamical model: a filtering problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 346-361
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Student processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 342-365
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
On Optimality of Bold Play for Primitive Casinos in the Presence of Inflation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 121-137
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Explicit Bounds for Approximation Rates of Boundary Crossing Probabilities for the Wiener Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 82-92
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Tools to Estimate the First Passage Time to a Convex Barrier
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 61-81
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Asymptotic Probabilities of an Exceedance Over Renewal Thresholds with an Application to Risk Theory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 153-162
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Kalman-Bucy Filtering for Linear Systems Driven by the Cox Process with Shot Noise Intensity and Its Application to the Pricing of Reinsurance Contracts
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 93-107
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Generalised shot noise Cox processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 48-74
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
What is Known About Robbins' Problem?
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 108-120
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Reflected backward stochastic differential equations under monotonicity and general increasing growth conditions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 134-159
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
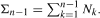 It is shown that the probability that the maximum
It is shown that the probability that the maximum 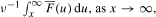 as
as 