Refine listing
Actions for selected content:
1830 results in 60Gxx
On-line selection of an acceptable pair
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 729-740
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
A martingale characterization of Pólya-Lundberg processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 741-754
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Limiting crossing probabilities of random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 884-891
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Bounds for perpetual American option prices in a jump diffusion model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 867-873
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Applications of factorization embeddings for Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 768-791
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
A more comprehensive complementary theorem for the analysis of Poisson point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 581-601
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Normal approximation for random sums
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 693-728
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Imperfect maintenance in a generalized competing risks framework
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 825-839
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Stationary partitions and Palm probabilities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 602-620
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Generating stationary random graphs on ℤ with prescribed independent, identically distributed degrees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 287-298
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
On a random-coefficient AR(1) process with heavy-tailed renewal switching coefficient and heavy-tailed noise
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 421-440
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Tail behavior of negatively associated heavy-tailed sums
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 587-593
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Fractional Laplace motion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 451-464
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Sufficient conditions for stability of longest-queue-first scheduling: second-order properties using fluid limits
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 505-521
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Slepian models for the stochastic shape of individual Lagrange sea waves
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 430-450
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Boundedly rational quasi-Bayesian learning in coordination games with imperfect monitoring
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 335-350
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Stability of spatial queueing systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 487-504
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Stationary-increment Student and variance-gamma processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 441-453
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
A simple integer-valued bilinear time series model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 559-578
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
An optimal sequential procedure for a buying-selling problem with independent observations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 454-462
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
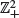 , with long-range weak dependence for each coordinate individually, usually present clustering of high values. For each one of the eight directions in
, with long-range weak dependence for each coordinate individually, usually present clustering of high values. For each one of the eight directions in 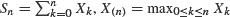 , and
, and 