Refine listing
Actions for selected content:
1829 results in 60Gxx
On extreme ruinous behaviour of Lévy insurance risk processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 594-598
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Rare events, temporal dependence, and the extremal index
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 463-485
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
The dead leaves model: a general tessellation modeling occlusion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 31-46
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Limit Theorems for Moving Averages with Random Coefficients and Heavy-Tailed Noise
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 245-256
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Monte Carlo Algorithms for Finding the Maximum of a Random Walk with Negative Drift
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 74-86
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Gambling Teams and Waiting Times for Patterns in Two-State Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 127-140
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
A Note on the Extremal Index for Space-Time Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 114-126
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Exponential Behavior in the Presence of Dependence in Risk Theory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 257-273
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
On regular variation for infinitely divisible random vectors and additive processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 134-148
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Numerical bounds for the distributions of the maxima of some one- and two-parameter Gaussian processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 149-170
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
A Forward Algorithm for Solving Optimal Stopping Problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 102-113
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
On Maxima and Ladder Processes for a Dense Class of Lévy Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 208-220
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
An Explicit Formula for the Optimal Gain in the Full-Information Problem of Owning a Relatively Best Object
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 87-101
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Rooted edges of a minimal directed spanning tree on random points
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-30
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
A class of self-similar random measure
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 908-914
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Extremes of regularly varying Lévy-driven mixed moving average processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 993-1014
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
On a localization property of wavelet coefficients for processes with stationary increments, and applications. I. Localization with respect to shift
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 938-962
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
A uniformly convergent adaptive particle filter
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1053-1068
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
The time to ruin for a class of Markov additive risk process with two-sided jumps
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 963-992
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
A renewal-process-type expression for the moments of inverse subordinators
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1134-1144
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
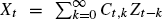 , generated by an array, {
, generated by an array, {