Refine listing
Actions for selected content:
1829 results in 60Gxx
The Palm-duality for random subsets of d-dimensional grids
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 318-325
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Heavy Tails of Discounted Aggregate Claims in the Continuous-Time Renewal Model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 285-294
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Winning Rate in the Full-Information Best-Choice Problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 560-565
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
On the Pricing of American Options in Exponential Lévy Markets
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 409-419
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Integrated Fractional white Noise as an Alternative to Multifractional Brownian Motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 393-408
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
A weighted random walk model, with application to a genetic algorithm
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 550-568
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Some distributional results for Poisson-Voronoi tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 16-40
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
The surface pair correlation function for stationary Boolean models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-15
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
On Two Damage Accumulation Models and Their Size Effects
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 99-114
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Stochastic stability of some state-dependent growth-collapse processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 189-220
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Renewal of singularity sets of random self-similar measures
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 162-188
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
On Threshold Strategies and the Smooth-Fit Principle for Optimal Stopping Problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 181-198
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
On Optimality of Bold Play for Discounted Dubins-Savage Gambling Problems with Limited Playing Times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 212-225
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Local asymptotics of the cycle maximum of a heavy-tailed random walk
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 221-244
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Continuous-time methods in the study of discretely sampled functionals of Lévy processes. I. The positive process case
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 245-270
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Thou Shalt not Diversify: Why ‘Two Of Every Sort’?
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 58-70
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
A connection between the volume fractions of the Stienen model and the dead leaves model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 41-52
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Optimal Strategy for the Vardi Casino with Interest Payments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 199-211
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Comparison Results for Branching Processes in Random Environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 142-150
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
General convex stochastic orderings and related martingale-type structures
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 105-127
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
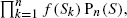 where the function
where the function 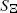 of a stationary Boolean model
of a stationary Boolean model 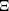 with grains from the convex ring is considered. A sufficient condition and a necessary condition for the existence of the density of the second-order moment measure of
with grains from the convex ring is considered. A sufficient condition and a necessary condition for the existence of the density of the second-order moment measure of 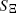 are given and a representation of this density is derived. As applications, the surface pair correlation functions of a Boolean model with spheres and a Boolean model with randomly oriented right circular cylinders in ℝ
are given and a representation of this density is derived. As applications, the surface pair correlation functions of a Boolean model with spheres and a Boolean model with randomly oriented right circular cylinders in ℝ