Refine listing
Actions for selected content:
1830 results in 60Gxx
The Large Deviation Principle for the On-Off Weibull Sojourn Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 107-117
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Sums of Dependent Nonnegative Random Variables with Subexponential Tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 85-94
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
The Pareto Copula, Aggregation of Risks, and the Emperor's Socks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 67-84
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Precise Large Deviations for Sums of Random Variables with Consistently Varying Tails in Multi-Risk Models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 889-900
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
On weak stationarity and weak isotropy of processes of convex bodies and cylinders
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 864-882
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
On the correlation between the volumes of the typical Poisson-Voronoi cell and the typical Stienen sphere
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 883-892
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
A note on the motion of an Ocean Bacterium in a Linear Shear Flow
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 157-160
- Print publication:
- December 2007
-
- Article
- Export citation
Wave intensities and slopes in Lagrangian seas
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1020-1035
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Optimal Stopping with Rank-Dependent Loss
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 996-1011
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
An Exponential Continuous-Time GARCH Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 960-976
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Moments of Random Allocation Processes Reaching a Boundary
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 990-995
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Functional limit theorems for critical processes with immigration
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1054-1069
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Bartlett spectrum and mixing properties of infinitely divisible random measures
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 893-897
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
A Gamma Activity Time Process with Noninteger Parameter and Self-Similar Limit
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 950-959
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Exit Problems for Spectrally Negative Lévy Processes Reflected at Either the Supremum or the Infimum
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1012-1030
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
On Utility-Based Superreplication Prices of Contingent Claims with Unbounded Payoffs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 880-888
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
On a Model for the Storage of Files on a Hardware. II. Evolution of a Typical Data Block
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 901-927
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Asymptotics for local maximal stack scores with general loop penalty function
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 776-798
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Asymptotic Behavior of a Generalized TCP Congestion Avoidance Algorithm
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 618-635
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
r-scan statistics of a Poisson process with events transformed by duplications, deletions, and displacements
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 799-825
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
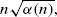 where α(
where α(