Refine listing
Actions for selected content:
1830 results in 60Gxx
Finite-time ruin probability with an exponential Lévy process investment return and heavy-tailed claims
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 206-224
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Optimal Stopping of a Brownian Bridge
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 170-180
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
From damage models to SIR epidemics and cascading failures
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 247-269
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
A discrete-time approximation for doubly reflected BSDEs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 101-130
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Monte Carlo methods for backward equations in nonlinear filtering
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 63-100
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
An Optimal Dividends Problem with a Terminal Value for Spectrally Negative Lévy Processes with a Completely Monotone Jump Density
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 85-98
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Bounds for the Distance Between the Distributions of Sums of Absolutely Continuous i.i.d. Convex-Ordered Random Variables with Applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 255-271
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
A Continuous-Time Approach to Robbins' Problem of Minimizing the Expected Rank
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-18
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
On the First Passage time for Brownian Motion Subordinated by a Lévy Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 181-198
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Dependent Risk Models with Bivariate Phase-Type Distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 113-131
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
An Integral-Equation Approach for Defaultable Bond Prices with Application to Credit Spreads
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 71-84
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
PRODUCT FRACTAL SETS DETERMINED BY STABLE PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 26 February 2009, pp. 201-212
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Analysis of stochastic fluid queues driven by local-time processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1072-1103
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
On Nonoptimality of Bold Play for Subfair Red-And-Black with a Rational-Valued House Limit
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1024-1038
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Continuous-State Branching Processes and Self-Similarity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1140-1160
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
State-dependent importance sampling for regularly varying random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1104-1128
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Chaoticity for Multiclass Systems and Exchangeability Within Classes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1196-1203
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
On the Correlation Structure of a Lévy-Driven Queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 940-952
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
On Asymptotics of Exchangeable Coalescents with Multiple Collisions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1186-1195
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Tails of Stopped Random Products: The Factoid and Some Relatives
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1161-1180
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
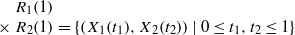 . The result of Hu generalizes [Some fractal sets determined by stable processes,
. The result of Hu generalizes [Some fractal sets determined by stable processes, 