In this paper we examine the extremal tail probabilities of moving sums in a marked Poisson random field. These sums are computed by adding up the weighted occurrences of events lying within a scanning set of fixed shape and size. We also provide an alternative representation of the constants of the asymptotic formulae in terms of the occupation measure of the conditional local random field at zero, and extend these representations to the constants of asymptotic tail probabilities of Gaussian random fields.

Directionally convex ordering is a useful tool for comparing the dependence structure of random vectors, which also takes into account the variability of the marginal distributions. It can be extended to random fields by comparing all finite-dimensional distributions. Viewing locally finite measures as nonnegative fields of measure values indexed by the bounded Borel subsets of the space, in this paper we formulate and study directionally convex ordering of random measures on locally compact spaces. We show that the directionally convex order is preserved under some of the natural operations considered on random measures and point processes, such as deterministic displacement of points, independent superposition, and thinning, as well as independent, identically distributed marking. Further operations on Cox point processes such as position-dependent marking and displacement of points are shown to preserve the order. We also examine the impact of the directionally convex order on the second moment properties, in particular on clustering and on Palm distributions. Comparisons of Ripley's functions and pair correlation functions, as well as examples, seem to indicate that point processes higher in the directionally convex order cluster more. In our main result we show that nonnegative integral shot noise fields with respect to the directionally convex ordered random measures inherit this ordering from the measures. Numerous applications of this result are shown, in particular to comparison of various Cox processes and some performance measures of wireless networks, in both of which shot noise fields appear as key ingredients. We also mention a few pertinent open questions.

We study lower-dimensional volume-weighted typical faces of a stationary Poisson hyperplane tessellation in d-dimensional Euclidean space. After showing how their distribution can be derived from that of the zero cell, we obtain sharp lower and upper bounds for the expected vertex number of the volume-weighted typical k-face (k=2,…,d). The bounds are respectively attained by parallel mosaics and by isotropic tessellations. We conclude with a remark on expected face numbers and expected intrinsic volumes of the zero cell.

In this paper we study a generalized Pólya urn with balls of two colors and a random triangular replacement matrix. We extend some results of Janson (2004), (2005) to the case where the largest eigenvalue of the mean of the replacement matrix is not in the dominant class. Using some useful martingales and the embedding method introduced in Athreya and Karlin (1968), we describe the asymptotic composition of the urn after the nth draw, for large n.

The trading strategy of ‘buy-and-hold for superior stock and sell-at-once for inferior stock’, as suggested by conventional wisdom, has long been prevalent in Wall Street. In this paper, two rationales are provided to support this trading strategy from a purely mathematical standpoint. Adopting the standard binomial tree model (or CRR model for short, as first introduced in Cox, Ross and Rubinstein (1979)) to model the stock price dynamics, we look for the optimal stock selling rule(s) so as to maximize (i) the chance that an investor can sell a stock precisely at its ultimate highest price over a fixed investment horizon [0,T]; and (ii) the expected ratio of the selling price of a stock to its ultimate highest price over [0,T]. We show that both problems have exactly the same optimal solution which can literally be interpreted as ‘buy-and-hold or sell-at-once’ depending on the value of p (the going-up probability of the stock price at each step): when p›½, selling the stock at the last time step N is the optimal selling strategy; when p=½, a selling time is optimal if the stock is sold either at the last time step or at the time step when the stock price reaches its running maximum price; and when p‹½, time 0, i.e. selling the stock at once, is the unique optimal selling time.

Convolutions of long-tailed and subexponential distributions play a major role in the analysis of many stochastic systems. We study these convolutions, proving some important new results through a simple and coherent approach, and also showing that the standard properties of such convolutions follow as easy consequences.

We study the tail behavior of the distribution of the sum of asymptotically independent risks whose marginal distributions belong to the maximal domain of attraction of the Gumbel distribution. We impose conditions on the distribution of the risks (X, Y) such that P(X + Y > x) ∼ (constant) P(X > x). With the further assumption of nonnegativity of the risks, the result is extended to more than two risks. We note a sufficient condition for a distribution to belong to both the maximal domain of attraction of the Gumbel distribution and the subexponential class. We provide examples of distributions which satisfy our assumptions. The examples include cases where the marginal distributions of X and Y are subexponential and also cases where they are not. In addition, the asymptotic behavior of linear combinations of such risks with positive coefficients is explored, leading to an approximate solution of an optimization problem which is applied to portfolio design.

In this paper we study the tail behavior of the maximum exceedance of a sequence of independent and identically distributed random variables over a random walk. For both light-tailed and heavy-tailed cases, we derive a precise asymptotic formula, which extends and unifies some existing results in the recent literature of applied probability.

In this paper we study the tail and the extremal behaviors of stationary solutions of threshold autoregressive (TAR) models. It is shown that a regularly varying noise sequence leads in general to only an O-regularly varying tail of the stationary solution. Under further conditions on the partition, it is shown however that TAR(S,1) models of order 1 with S regimes have regularly varying tails, provided that the noise sequence is regularly varying. In these cases, the finite-dimensional distribution of the stationary solution is even multivariate regularly varying and its extremal behavior is studied via point process convergence. In particular, a TAR model with regularly varying noise can exhibit extremal clusters. This is in contrast to TAR models with noise in the maximum domain of attraction of the Gumbel distribution and which is either subexponential or in ℒ(γ) with γ > 0. In this case it turns out that the tail of the stationary solution behaves like a constant times that of the noise sequence, regardless of the order and the specific partition of the TAR model, and that the process cannot exhibit clusters on high levels.

In this paper we consider the following problem. An angler buys a fishing ticket that allows him/her to fish for a fixed time. There are two locations to fish at the lake. The fish are caught according to a renewal process, which is different for each fishing location. The angler's success is defined as the difference between the utility function, which is dependent on the size of the fish caught, and the time-dependent cost function. These functions are different for each fishing location. The goal of the angler is to find two optimal stopping times that maximize his/her success: when to change fishing location and when to stop fishing. Dynamic programming methods are used to find these two optimal stopping times and to specify the expected success of the angler at these times.

In this article we analyse the behaviour of the extremes of a random walk in a random scenery. The random walk is assumed to be in the domain of attraction of a stable law, and the scenery is assumed to be in the domain of attraction of an extreme value distribution. The resulting random sequence is stationary and strongly dependent if the underlying random walk is recurrent. We prove a limit theorem for the extremes of the resulting stationary process. However, if the underlying random walk is recurrent, the limit distribution is not in the class of classical extreme value distributions.

Consider an urn model whose replacement matrix is triangular, has all nonnegative entries, and the row sums are all equal to 1. We obtain strong laws for the counts of balls corresponding to each color. The scalings for these laws depend on the diagonal elements of a rearranged replacement matrix. We use these strong laws to study further behavior of certain three-color urn models.

Chiu and Yin (2005) found the Laplace transform of the last time a spectrally negative Lévy process, which drifts to ∞, is below some level. The main motivation for the study of this random time stems from risk theory: what is the last time the risk process, modeled by a spectrally negative Lévy process drifting to ∞, is 0? In this paper we extend the result of Chiu and Yin, and we derive the Laplace transform of the last time, before an independent, exponentially distributed time, that a spectrally negative Lévy process (without any further conditions) exceeds (upwards or downwards) or hits a certain level. As an application, we extend a result found in Doney (1991).

In this paper we generalize existing results for the steady-state distribution of growth-collapse processes. We begin with a stationary setup with some relatively general growth process and observe that, under certain expected conditions, point- and time-stationary versions of the processes exist as well as a limiting distribution for these processes which is independent of initial conditions and necessarily has the marginal distribution of the stationary version. We then specialize to the cases where an independent and identically distributed (i.i.d.) structure holds and where the growth process is a nondecreasing Lévy process, and in particular linear, and the times between collapses form an i.i.d. sequence. Known results can be seen as special cases, for example, when the inter-collapse times form a Poisson process or when the collapse ratio is deterministic. Finally, we comment on the relation between these processes and shot-noise type processes, and observe that, under certain conditions, the steady-state distribution of one may be directly inferred from the other.

Suppose that an unknown number of objects arrive sequentially according to a Poisson process with random intensity λ on some fixed time interval [0,T]. We assume a gamma prior density G λ(r, 1/a) for λ. Furthermore, we suppose that all arriving objects can be ranked uniquely among all preceding arrivals. Exactly one object can be selected. Our aim is to find a stopping time (selection time) which maximizes the time during which the selected object will stay relatively best. Our main result is the following. It is optimal to select the ith object that is relatively best and arrives at some time s i (r) onwards. The value of s i (r) can be obtained for each r and i as the unique root of a deterministic equation.

Given a pure-jump subordinator (i.e. nondecreasing Lévy process with no drift) with continuous Lévy measure ν, we derive a formula for the distribution function F s (x; t) at time t of the associated subordinator whose Lévy measure is the restriction of ν to (0,s]. It will be expressed in terms of ν and the marginal distribution function F (⋅; t) of the original process. A generalization concerning an arbitrary truncation of ν will follow. Under certain conditions, an analogous formula will be obtained for the nth derivative, ∂n F s (x; t) ∂ x n . The requirement that ν is continuous is shown to have no intrinsic meaning. A number of interesting results involving the size ordered jumps of subordinators will be derived. An appropriate approximation for the small jumps of a gamma process will be considered, leading to a revisiting of the generalized Dickman distribution.

Convergence in probability and central limit laws of bipower variation for Gaussian processes with stationary increments and for integrals with respect to such processes are derived. The main tools of the proofs are some recent powerful techniques of Wiener/Itô/Malliavin calculus for establishing limit laws, due to Nualart, Peccati, and others.

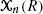Let n points be chosen independently and uniformly in the unit cube [0,1]d , and suppose that each point is supplied with a mark, the marks being independent and identically distributed random variables independent of the location of the points. To each cube R contained in [0,1]d we associate its score defined as the sum of marks of all points contained in 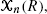R. The scan statistic is defined as the maximum of taken over all cubes R contained in [0,1]d . We show that if the marks are nonlattice random variables with finite exponential moments, having negative mean and assuming positive values with nonzero probability, then the appropriately normalized distribution of the scan statistic converges as n → ∞ to the Gumbel distribution. We also prove a corresponding result for the scan statistic of a Lévy noise with negative mean. The more elementary cases of zero and positive mean are also considered.

A gambler with an initial bankroll is faced with a finite sequence of identical and independent bets. For each bet, he may wager up to his current bankroll, and will win this amount with probability p or lose it with probability 1-p. His problem is to devise a wagering strategy that will maximize his final expected utility with the side condition that the total amount wagered (i.e. the total ‘action’) be at least his initial bankroll. Our main result is an expression that characterizes when the strategy of placing equal-sized wagers on all bets is optimal. In particular, for a given bankroll B, utility function f (concave, increasing, differentiable), and n bets, we show that it is optimal to wager b/n on each bet if and only if the probability of winning each bet is less than or equal to some value p ⋆∈[½,1] (where p ⋆ is an explicit function of B, f, and n). We prove the result by using a basic nonlinear programming technique.

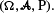Let I 1,I 2,…,I n be independent indicator functions on some probability space We suppose that these indicators can be observed sequentially. Furthermore, let 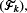T be the set of stopping times on (I k ), k=1,…,n, adapted to the increasing filtration where 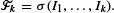The odds algorithm solves the problem of finding a stopping time τ ∈ 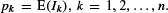T which maximises the probability of stopping on the last I k =1, if any. To apply the algorithm, we only need the odds for the events {I k =1}, that is, r k =p k /(1-p k ), where The goal of this paper is to offer tractable solutions for the case where the p k are unknown and must be sequentially estimated. The motivation is that this case is important for many real-world applications of optimal stopping. We study several approaches to incorporate sequential information. Our main result is a new version of the odds algorithm based on online observation and sequential updating. Questions of speed and performance of the different approaches are studied in detail, and the conclusiveness of the comparisons allows us to propose always using this algorithm to tackle selection problems of this kind.