Refine listing
Actions for selected content:
1830 results in 60Gxx
A Fourth Moment Inequality for Functionals of Stationary Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1086-1096
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
How Nearly do Arriving Customers See Time-Average Behavior?
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 963-971
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Entry and Exit Decision Problem with Implementation Delay
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1039-1059
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Multifractality of products of geometric Ornstein-Uhlenbeck-type processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1129-1156
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
A quadratic ARCH(∞) model with long memory and Lévy stable behavior of squares
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1198-1222
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Random Laguerre tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 630-650
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
On level crossings for a general class of piecewise-deterministic Markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 815-834
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
EVT-based estimation of risk capital and convergence of high quantiles
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 696-715
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Pricing of Catastrophe Insurance Options Under Immediate Loss Reestimation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 831-845
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Hitting Time and Inverse Problems for Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 640-649
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
A new metric between distributions of point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 651-672
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Moment and MGF convergence of overshoots and undershoots for Lévy insurance risk processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 716-733
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
First Passage Times for Markov Additive Processes with Positive Jumps of Phase Type
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 779-799
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Assessing a Linear Nanosystem's Limiting Reliability from its Components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 879-887
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
The Generalised Coupon Collector Problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 621-629
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Functional Large Deviations and Moderate Deviations for Markov-Modulated Risk Models with Reinsurance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 800-817
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Lévy-based Cox point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 603-629
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
A functional central limit theorem for spatial birth and death processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 759-797
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
REAL ZEROS OF ALGEBRAIC POLYNOMIALS WITH STABLE RANDOM COEFFICIENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 81-86
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
AN Lp ‘COUSIN OF COBOUNDARY’ THEOREM FOR RANDOM FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 51-58
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
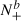 of upcrossings of some level
of upcrossings of some level 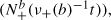 where ν
where ν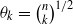 . The latter generate a polynomial with binomial elements which has recently been of significant interest and has previously been studied only for Gaussian distributed coefficients. We see the effect of
. The latter generate a polynomial with binomial elements which has recently been of significant interest and has previously been studied only for Gaussian distributed coefficients. We see the effect of 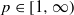 and a given strictly stationary sequence of random variables, the
and a given strictly stationary sequence of random variables, the 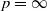 is included.
is included.