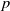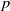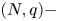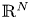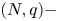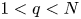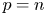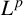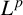Refine listing
Actions for selected content:
101 results in 26Dxx
Sharp Hardy and spectral gap inequalities on special irreversible Finsler manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-36
-
- Article
- Export citation
Existence of minimizers of the stability constant of Caffarelli–Kohn–Nirenberg inequality
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-23
-
- Article
- Export citation
ON SOME EFFECTIVE RESULTS INVOLVING ZEROS OF THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 21 March 2025, pp. 563-565
- Print publication:
- June 2025
-
- Article
-
- You have access
- HTML
- Export citation
On discrete reversed Hardy–Littlewood–Sobolev inequalities
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 14 March 2025, pp. 1025-1036
- Print publication:
- December 2025
-
- Article
- Export citation
Improvement of some discrete Hardy inequalities with variants
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 114-130
- Print publication:
- January 2025
-
- Article
- Export citation
Sobolev trace-type inequalities via time-space fractional heat equations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1093-1134
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multidimensional Frank–Laptev–Weidl improvement of the hardy inequality
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 151-167
-
- Article
- Export citation
A weighted Trudinger–Moser inequalities and applications to some weighted $(N,q)-$
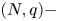 Laplacian equation in $\mathbb {R}^N$
Laplacian equation in $\mathbb {R}^N$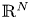 with new exponential growth conditions
with new exponential growth conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 124-175
- Print publication:
- February 2025
-
- Article
- Export citation
Shape sensitivity of the Hardy constant involving the distance from a boundary submanifold
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 22 February 2023, pp. 408-423
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REVERSED HARDY–LITTLEWOOD–PÓLYA INEQUALITIES WITH FINITE TERMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 03 February 2023, pp. 459-463
- Print publication:
- December 2023
-
- Article
- Export citation
The Halász–Székely barycenter
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 13 October 2022, pp. 881-911
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a class of Hilbert-type inequalities in the whole plane involving some classical kernel functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 06 October 2022, pp. 833-846
-
- Article
- Export citation
106.29 An improvement on the Garfunkel-Bankoff inequality
- Part of
-
- Journal:
- The Mathematical Gazette / Volume 106 / Issue 566 / July 2022
- Published online by Cambridge University Press:
- 22 June 2022, pp. 342-344
- Print publication:
- July 2022
-
- Article
- Export citation
Series expansion of Leray–Trudinger inequality
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 20 December 2021, pp. 262-274
- Print publication:
- February 2023
-
- Article
- Export citation
Lorentz and Gale–Ryser theorems on general measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 09 August 2021, pp. 857-878
- Print publication:
- August 2022
-
- Article
- Export citation
SOME
 $\boldsymbol {L^p}$-HARDY AND
$\boldsymbol {L^p}$-HARDY AND  $\boldsymbol {L^p}$-RELLICH TYPE INEQUALITIES WITH REMAINDER TERMS
$\boldsymbol {L^p}$-RELLICH TYPE INEQUALITIES WITH REMAINDER TERMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 22 June 2021, pp. 79-98
- Print publication:
- August 2022
-
- Article
- Export citation
EMBEDDING THEOREM OF THE WEIGHTED SOBOLEV–LORENTZ SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 358-375
- Print publication:
- May 2022
-
- Article
- Export citation
Log-concavity and log-convexity of moments of averages of i.i.d. random variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 271-278
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting matchings via capacity-preserving operators
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 956-981
-
- Article
-
- You have access
- Open access
- Export citation
On finite sections of the multiplicative Hilbert inequalities
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 208-216
- Print publication:
- March 2022
-
- Article
- Export citation