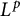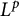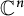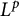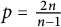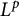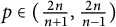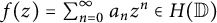Refine listing
Actions for selected content:
98 results in 32Axx
Sobolev regularity of the Bergman projection on a class of singular Reinhardt domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 September 2025, pp. 1-17
-
- Article
- Export citation
Entire solutions of product type nonlinear partial differential equations in
 $\mathbb{C}^n$
$\mathbb{C}^n$
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 12 August 2025, pp. 1-6
-
- Article
- Export citation
Deformed Aeppli cohomology: canonical deformations and jumping formulas
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-34
-
- Article
- Export citation
The Schur–Agler class in infinitely many variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
At the crossroads of holomorphic dynamic and operator theory: spectral properties of composition operators on
 $\mathrm {Hol}(\mathbb {B}_N)$
$\mathrm {Hol}(\mathbb {B}_N)$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 11 June 2025, pp. 1289-1314
- Print publication:
- December 2025
-
- Article
- Export citation
On meromorphic solutions of certain partial differential equations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1177-1191
- Print publication:
- December 2025
-
- Article
- Export citation
A note on composition operators on the disc and bidisc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1163-1176
- Print publication:
- December 2025
-
- Article
- Export citation
Burns-Krantz rigidity in non-smooth domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1037-1046
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compact composition operators on model spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1109-1115
- Print publication:
- December 2025
-
- Article
- Export citation
GAUSSIAN HOLOMORPHIC SECTIONS ON NONCOMPACT COMPLEX MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 1197-1262
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On spectra of Hankel operators on the polydisc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 301-317
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Defect relation for holomorphic maps from complex discs into projective varieties and hypersurfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 157-172
-
- Article
- Export citation
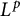 $L^p$ regularity of the Bergman projection on the symmetrized polydisc
$L^p$ regularity of the Bergman projection on the symmetrized polydisc
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 22 October 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $L^p$-BOUNDEDNESS OF THE BEREZIN TRANSFORM ON GENERALISED HARTOGS TRIANGLES
$L^p$-BOUNDEDNESS OF THE BEREZIN TRANSFORM ON GENERALISED HARTOGS TRIANGLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 541-551
- Print publication:
- June 2025
-
- Article
- Export citation
Characterization of continuous homomorphisms on entire slice monogenic functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 17 May 2024, pp. 892-920
-
- Article
- Export citation
Dirichlet-type spaces of the unit bidisc and toral 2-isometries
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1271-1293
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CLASS OF SYMBOLS THAT INDUCE BOUNDED COMPOSITION OPERATORS FOR DIRICHLET-TYPE SPACES ON THE DISC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 14 March 2024, pp. 140-145
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The degree one Laguerre–Pólya class and the shuffle-word-embedding conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 760-767
- Print publication:
- September 2024
-
- Article
- Export citation
A characterization of random analytic functions satisfying Blaschke-type conditions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 17 January 2024, pp. 670-679
- Print publication:
- September 2024
-
- Article
- Export citation
Trigonometric convexity of the multidimensional indicator
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 05 January 2024, pp. 384-399
- Print publication:
- April 2025
-
- Article
- Export citation