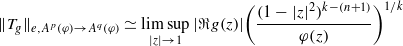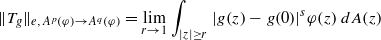Refine listing
Actions for selected content:
98 results in 32Axx
HOLOMORPHIC AUTOMORPHISMS AND PROPER HOLOMORPHIC SELF-MAPPINGS OF A TYPE OF GENERALISED MINIMAL BALL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 18 August 2017, pp. 455-467
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
INTEGRAL MEANS OF HOLOMORPHIC FUNCTIONS AS GENERIC LOG-CONVEX WEIGHTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 07 August 2017, pp. 88-93
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
 $\unicode[STIX]{x1D6F7}$ -CARLESON MEASURES AND MULTIPLIERS BETWEEN BERGMAN–ORLICZ SPACES OF THE UNIT BALL OF
$\unicode[STIX]{x1D6F7}$ -CARLESON MEASURES AND MULTIPLIERS BETWEEN BERGMAN–ORLICZ SPACES OF THE UNIT BALL OF  $\mathbb{C}^{n}$
$\mathbb{C}^{n}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 22 March 2017, pp. 63-79
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
DISCREPANCY OF SECOND ORDER DIGITAL SEQUENCES IN FUNCTION SPACES WITH DOMINATING MIXED SMOOTHNESS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 863-894
- Print publication:
- 2017
-
- Article
- Export citation
THE HILBERT–SCHMIDT NORM OF A COMPOSITION OPERATOR ON THE BERGMAN SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 250-259
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
SPLITTING INVARIANT SUBSPACES IN THE HARDY SPACE OVER THE BIDISK
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 12 May 2016, pp. 205-223
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
SEMIGROUPS OF COMPOSITION OPERATORS ON LOCAL DIRICHLET SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 144-154
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
EXTENSION AND RESTRICTION FOR BERGMAN SCALE OF SPACES AND ONE-DIMENSIONAL SUBVARIETIES ON CONVEX FINITE TYPE DOMAINS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 221 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 15 March 2016, pp. 165-183
- Print publication:
- March 2016
-
- Article
-
- You have access
- HTML
- Export citation
ON THE KÄHLER–EINSTEIN METRIC OF BERGMAN–HARTOGS DOMAINS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 221 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 15 March 2016, pp. 184-206
- Print publication:
- March 2016
-
- Article
-
- You have access
- HTML
- Export citation
Application and simplified proof of a sharp L2 extension theorem
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 220 / December 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 81-89
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
HELSON’S PROBLEM FOR SUMS OF A RANDOM MULTIPLICATIVE FUNCTION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 21 October 2015, pp. 101-110
- Print publication:
- 2016
-
- Article
- Export citation
BOUNDED TOEPLITZ AND HANKEL PRODUCTS ON THE WEIGHTED BERGMAN SPACES OF THE UNIT BALL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 05 June 2015, pp. 237-249
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
TOEPLITZ OPERATORS BETWEEN FOCK SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 02 June 2015, pp. 316-324
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Normal families of meromorphic mappings of several complex variables for moving hypersurfaces in a complex projective space
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 217 / March 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 23-59
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
AN INTEGRAL REPRESENTATION FOR BESOV AND LIPSCHITZ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 17 October 2014, pp. 129-144
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
Normal crossing properties of complex hypersurfaces via logarithmic residues
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 9 / September 2014
- Published online by Cambridge University Press:
- 25 June 2014, pp. 1607-1622
- Print publication:
- September 2014
-
- Article
- Export citation
THE TUMURA–CLUNIE THEOREM IN SEVERAL COMPLEX VARIABLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 444-456
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
KORÁNYI’S LEMMA FOR HOMOGENEOUS SIEGEL DOMAINS OF TYPE II. APPLICATIONS AND EXTENDED RESULTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 13 May 2014, pp. 77-89
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
ESSENTIAL NORM OF EXTENDED CESÀRO OPERATORS FROM ONE BERGMAN SPACE TO ANOTHER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 12 December 2011, pp. 307-314
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
COMPACT DIFFERENCES OF COMPOSITION OPERATORS ON BERGMAN SPACES IN THE BALL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 14 March 2011, pp. 407-418
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
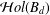
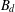
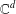
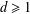
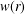
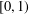
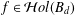
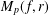
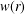
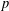
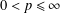
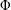
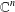
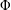
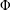
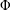
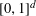
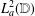
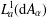

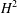
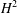
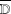
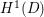
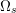
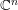

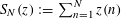
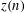
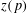
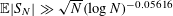
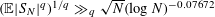

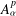
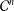
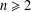
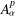
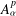
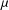

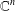
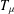
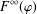
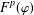
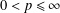

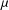
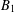
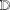
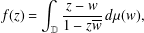
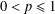
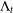
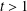
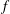
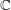
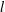
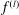
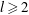
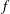
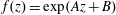
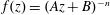
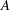
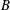
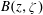

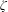
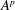
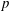
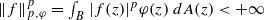 , where φ is a given normal weight. Let
, where φ is a given normal weight. Let 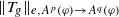 . In this paper it is proved that, for
. In this paper it is proved that, for