Refine listing
Actions for selected content:
98 results in 32Axx
FAMILIES OF FRACTIONAL FANTAPPIÈ TRANSFORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 07 April 2010, pp. 62-78
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
COMPOSITION OPERATORS BELONGING TO SCHATTEN CLASS 𝒮p
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 17 March 2010, pp. 465-472
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
On the Asymptotic Behavior of Complete Kähler Metrics of Positive Ricci Curvature
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-18
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
DIFFERENCES OF COMPOSITION OPERATORS ON THE BLOCH SPACE IN THE POLYDISC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 465-471
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
THE RATE OF INCREASE OF MEAN VALUES OF FUNCTIONS IN HARDY SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 199-204
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Composition operators on μ-Bloch spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 1 / 01 February 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 50-75
- Print publication:
- 01 February 2009
-
- Article
-
- You have access
- Export citation
ON R-SECTORIAL DERIVATIVES ON BERGMAN SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 305-313
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
A note on the boundedness of Bergman-type operators on mixed norm spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 395-402
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
The Exponential Representation of Holomorphic Functions of Uniformly Bounded Type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 235-246
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
A characterization of weighted Bergman-Orlicz spaces on the unit ball in Cn
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 5-18
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
The Lindelöf principle and angular derivatives in convex domains of finite type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 221-250
- Print publication:
- October 2002
-
- Article
-
- You have access
- Export citation
Transformation formula of higher order integrals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 155-164
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
A Generalization of the Schwarz Lemma to Normal Selfaps of Complex Spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 10-18
- Print publication:
- February 2000
-
- Article
-
- You have access
- Export citation
The Möbius boundedness of the space Qp
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 373-378
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
Invariant subspaces in the bidisc and commutators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 232-242
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Integral formulas with weight factors
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 1 / February 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 26-39
- Print publication:
- February 1992
-
- Article
-
- You have access
- Export citation
Multidimensional Volterra integral equations of convolution type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 3 / May 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 305-312
- Print publication:
- May 1979
-
- Article
-
- You have access
- Export citation
Inner functions and the maximal ideal space of L∞(Tn)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 26 / Issue 2 / September 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 175-178
- Print publication:
- September 1978
-
- Article
-
- You have access
- Export citation
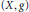
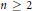

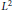
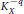

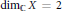
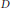
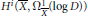
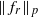 as
as 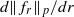 grows at most like
grows at most like 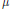
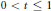
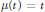
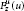
 ” with an application to Gleason's problem.
” with an application to Gleason's problem.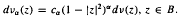 Here
Here 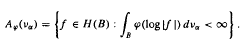
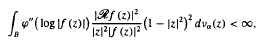 where
where 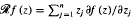 is the radial derivative of
is the radial derivative of 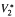 , For example, M is studied when the commutator is self-adjoint or of finite rank.
, For example, M is studied when the commutator is self-adjoint or of finite rank.