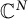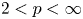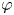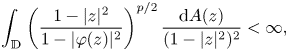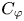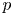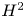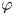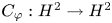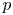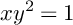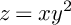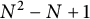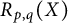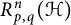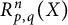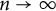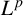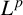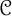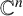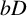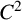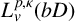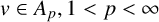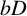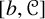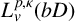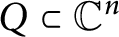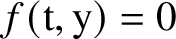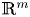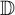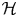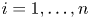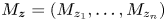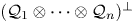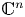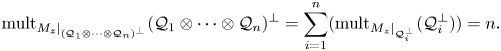Refine listing
Actions for selected content:
98 results in 32Axx
Linear fractional self-maps of the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 November 2023, pp. 458-468
- Print publication:
- June 2024
-
- Article
- Export citation
ON THE EXCEPTIONAL SET OF TRANSCENDENTAL ENTIRE FUNCTIONS IN SEVERAL VARIABLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 64-71
- Print publication:
- August 2024
-
- Article
- Export citation
Schatten class composition operators on the Hardy space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1364-1377
- Print publication:
- October 2024
-
- Article
- Export citation
Uncertainty principles in holomorphic function spaces on the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 122-136
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A logarithmic lower bound for the second Bohr radius
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 27 June 2023, pp. 90-93
- Print publication:
- March 2024
-
- Article
- Export citation
ERRATUM TO “NON-UNIFORMLY FLAT AFFINE ALGEBRAIC HYPERSURFACES”
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 252 / December 2023
- Published online by Cambridge University Press:
- 06 June 2023, pp. 985-989
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
Determining sets for holomorphic functions on the symmetrized bidisk
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 984-996
- Print publication:
- September 2023
-
- Article
- Export citation
A note on cyclic vectors in Dirichlet-type spaces in the unit ball of
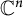 ${\mathbb C}^n$
${\mathbb C}^n$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 January 2023, pp. 886-902
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Estimates for generalized Bohr radii in one and higher dimensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 04 November 2022, pp. 682-699
- Print publication:
- June 2023
-
- Article
- Export citation
A polynomial approximation result for free Herglotz–Agler functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 October 2022, pp. 665-678
- Print publication:
- June 2023
-
- Article
- Export citation
Some remarks on approximation in several complex variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 October 2022, pp. 643-653
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\boldsymbol {L^{p}}$ REGULARITY OF THE SZEGÖ PROJECTION ON THE SYMMETRISED POLYDISC
$\boldsymbol {L^{p}}$ REGULARITY OF THE SZEGÖ PROJECTION ON THE SYMMETRISED POLYDISC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 12 May 2022, pp. 481-490
- Print publication:
- December 2022
-
- Article
- Export citation
BOUNDEDNESS AND COMPACTNESS OF CAUCHY-TYPE INTEGRAL COMMUTATOR ON WEIGHTED MORREY SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 08 March 2022, pp. 36-56
- Print publication:
- August 2022
-
- Article
- Export citation
Operator valued analogues of multidimensional Bohr’s inequality
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 1020-1035
- Print publication:
- December 2022
-
- Article
- Export citation
Arquile Varieties – Varieties Consisting of Power Series in a Single Variable
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 01 December 2021, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A criterion for normality of analytic mappings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 19 November 2021, pp. 80-88
-
- Article
- Export citation
Slices of parameter space for meromorphic maps with two asymptotic values
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 99-139
- Print publication:
- January 2023
-
- Article
- Export citation
Asymptotic first boundary value problem for holomorphic functions of several complex variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 361-380
- Print publication:
- June 2022
-
- Article
- Export citation
Multiplicities, invariant subspaces and an additive formula
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 279-297
-
- Article
- Export citation
Volume integral means over spherical shell
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 12 April 2021, pp. 180-197
- Print publication:
- March 2022
-
- Article
- Export citation