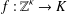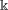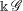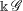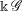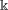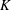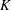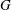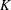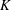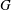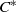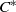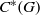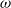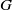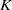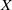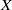Refine listing
Actions for selected content:
73 results in 22Axx
ON GENERALISED METRISABILITY AND CARDINAL INVARIANTS IN QUASITOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 17 October 2018, pp. 302-310
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
On Følner sets in topological groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1333-1361
- Print publication:
- July 2018
-
- Article
- Export citation
CHAIN CONDITIONS ON ÉTALE GROUPOID ALGEBRAS WITH APPLICATIONS TO LEAVITT PATH ALGEBRAS AND INVERSE SEMIGROUP ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 403-411
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
DENSITY, SMITAL PROPERTY AND QUASICONTINUITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 246-252
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
ON VARIETIES OF ABELIAN TOPOLOGICAL GROUPS WITH COPRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 54-65
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
AN OPEN MAPPING THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 65-69
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
A NOTE ON PSEUDOVARIETIES OF COMPLETELY REGULAR SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 233-237
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
META-CENTRALIZERS OF NON-LOCALLY COMPACT GROUP ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 349-364
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
MODULES OVER ÉTALE GROUPOID ALGEBRAS AS SHEAVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 418-429
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A NOTE ON
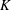 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-SPACES
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 144-148
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Cartan subgroups of groups definable ino-minimal structures
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 28 November 2013, pp. 849-893
- Print publication:
- October 2014
-
- Article
- Export citation
GROUPOID
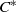 ${C}^{\ast } $-ALGEBRAS WITH HAUSDORFF SPECTRUM
${C}^{\ast } $-ALGEBRAS WITH HAUSDORFF SPECTRUM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 232-242
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
NOTES ON
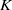 $K$-TOPOLOGICAL GROUPS AND HOMEOMORPHISMS OF TOPOLOGICAL GROUPS
$K$-TOPOLOGICAL GROUPS AND HOMEOMORPHISMS OF TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 30 August 2012, pp. 493-502
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
WHAT IS THE HIGHER-DIMENSIONAL INFINITESIMAL GROUPOID OF A MANIFOLD?
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 14 June 2011, pp. 155-170
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
Étale groupoids as germ groupoids and their base extensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 05 August 2010, pp. 765-785
-
- Article
-
- You have access
- Export citation
VARIETIES OF ABELIAN TOPOLOGICAL GROUPS AND SCATTERED SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 487-495
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
CONTINUITY OF MEASURABLE HOMOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 171-176
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
Cohomology of topological groups with applications to the Weil group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 633-656
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
An Open Mapping Theorem For Pro-Lie Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-78
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
Local Homomorphisms of Topological Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 135-148
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation