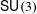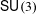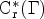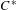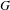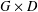Refine listing
Actions for selected content:
97 results in 22Dxx
The mapping class group action on
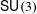 $\mathsf{SU}(3)$-character varieties
$\mathsf{SU}(3)$-character varieties
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 15 June 2020, pp. 2382-2396
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
A new characterization of the Haagerup property by actions on infinite measure spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 2349-2368
- Print publication:
- August 2021
-
- Article
- Export citation
DECOMPOSITION THEOREMS FOR AUTOMORPHISM GROUPS OF TREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 May 2020, pp. 104-112
- Print publication:
- February 2021
-
- Article
- Export citation
STABILITY, COHOMOLOGY VANISHING, AND NONAPPROXIMABLE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 March 2020, e18
-
- Article
-
- You have access
- Open access
- Export citation
Amenable uniformly recurrent subgroups and lattice embeddings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 07 February 2020, pp. 1464-1501
- Print publication:
- May 2021
-
- Article
- Export citation
Super-rigidity and non-linearity for lattices in products
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 158-178
- Print publication:
- January 2020
-
- Article
- Export citation
BOREL DENSITY FOR APPROXIMATE LATTICES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 05 November 2019, e40
-
- Article
-
- You have access
- Open access
- Export citation
Bounding the covolume of lattices in products
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 11 October 2019, pp. 2296-2333
- Print publication:
- December 2019
-
- Article
- Export citation
On pathological properties of fixed point algebras in Kirchberg algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 20 September 2019, pp. 3087-3096
- Print publication:
- December 2020
-
- Article
- Export citation
On graph products of multipliers and the Haagerup property for
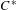 $C^{\ast }$-dynamical systems
$C^{\ast }$-dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 07 August 2019, pp. 3188-3216
- Print publication:
- December 2020
-
- Article
- Export citation
A GENERALISATION OF THE FROBENIUS RECIPROCITY THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 18 February 2019, pp. 317-322
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Induction for locally compact quantum groups revisited
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1071-1093
- Print publication:
- April 2020
-
- Article
- Export citation
Delone dynamical systems and spectral convergence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 22 October 2018, pp. 1510-1544
- Print publication:
- June 2020
-
- Article
- Export citation
Characters of inductive limits of finite alternating groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 04 September 2018, pp. 1068-1082
- Print publication:
- April 2020
-
- Article
- Export citation
OPERATOR ALGEBRAIC APPROACH TO INVERSE AND STABILITY THEOREMS FOR AMENABLE GROUPS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 98-118
- Print publication:
- 2019
-
- Article
- Export citation
LOCALLY COMPACT WREATH PRODUCTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 26-52
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
HARDY’S THEOREM FOR GABOR TRANSFORM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 143-159
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Subgroup Correspondences
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 14 August 2018, pp. 1127-1154
-
- Article
- Export citation
CHABAUTY LIMITS OF SIMPLE GROUPS ACTING ON TREES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1093-1120
- Print publication:
- July 2020
-
- Article
- Export citation
The Point Value Maximization Problem for Positive Definite Functions Supported in a Given Subset of a Locally Compact Group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 24 January 2018, pp. 179-200
-
- Article
- Export citation