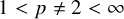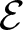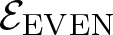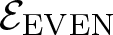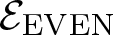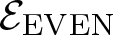Refine listing
Actions for selected content:
97 results in 22Dxx
Characterisation of Locally Compact Abelian Groups Having Spectral Synthesis
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 September 2025, e145
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On homological properties of the Schlichting completion
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 04 September 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PROPERTY (T) AND STRONG 1-BOUNDEDNESS FOR VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-34
-
- Article
- Export citation
CHARACTERISATION OF DISTAL ACTIONS OF AUTOMORPHISMS ON THE SPACE OF ONE-PARAMETER SUBGROUPS OF LIE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 15 August 2025, pp. 152-175
- Print publication:
- October 2025
-
- Article
- Export citation
Density and unitarity of the Burau representation from a non-semisimple TQFT
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-29
-
- Article
- Export citation
Locally compact modules over abelian groups and compactly generated metabelian groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1250-1283
- Print publication:
- June 2025
-
- Article
- Export citation
The local geometry of idempotent Schur multipliers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 March 2025, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDED CONJUGACY CLASSES AND CONJUGACY CLASSES SUPPORTING INVARIANT MEASURES AND AUTOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-6
-
- Article
- Export citation
ON EQUIVALENCE RELATIONS INDUCED BY POLISH GROUPS ADMITTING COMPATIBLE TWO-SIDED INVARIANT METRICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 February 2025, pp. 1-38
-
- Article
- Export citation
Closed approximate subgroups: compactness, amenability and approximate lattices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Szemerédi type theorem for sets of positive density in approximate lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2023-2053
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear repetitivity beyond abelian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1947-1997
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cross-sectional C*-algebras associated with subgroups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 December 2024, pp. 1-26
-
- Article
- Export citation
Transference of multilinear Fourier and Schur multipliers acting on noncommutative
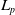 $L_p$-spaces for non-unimodular groups
$L_p$-spaces for non-unimodular groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 197-223
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The planar 3-colorable subgroup ε of Thompson’s group F and its even part
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 173-197
-
- Article
- Export citation
Entropy of group actions beyond uniform lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1461-1502
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE WEYL TRANSFORM OF A SMOOTH MEASURE ON A REAL-ANALYTIC SUBMANIFOLD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 184-193
- Print publication:
- August 2025
-
- Article
- Export citation
Connes fusion of spinors on loop space
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1596-1650
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak amenability for dual Banach algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 29 April 2024, pp. 740-748
-
- Article
- Export citation
SPHERICAL REPRESENTATIONS FOR
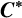 $\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
$\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 239-272
- Print publication:
- October 2024
-
- Article
- Export citation