Refine listing
Actions for selected content:
97 results in 22Dxx
Some irreducible free group representations in which a linear combination of the generators has an eigenvalue
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-286
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
On the Toeplitz algebras of right-angled and finite-type Artin groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-246
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
Scale functions and tree ends
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-292
- Print publication:
- April 2001
-
- Article
-
- You have access
- Export citation
On diameters of orbits of compact groups in unitary representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 308-312
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
On the component group of the automorphism group of a Lie group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-385
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
Twisted crossed products by coactions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 320-344
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
Cartan subalgebras of regular extensions of von Neumann algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 249-274
- Print publication:
- October 1988
-
- Article
-
- You have access
- Export citation
On the characters of unitary representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 62-65
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
Representations of minimally almost periodic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-375
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
The Akivis algebra of a homogeneous loop
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-95
- Print publication:
- June 1986
-
- Article
- Export citation
The ~ -representations of symmetric homogeneous algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 267-275
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation
Special series of unitary representations of groups acting on homogeneous trees
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 1 / February 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 83-88
- Print publication:
- February 1986
-
- Article
-
- You have access
- Export citation
Minimal F2-flows
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 187-193
- Print publication:
- October 1985
-
- Article
-
- You have access
- Export citation
Some groups with T1 primitive ideal spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-64
- Print publication:
- February 1985
-
- Article
-
- You have access
- Export citation
The von Neumann kernel of a locally compact group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 2 / April 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 279-286
- Print publication:
- April 1984
-
- Article
-
- You have access
- Export citation
Discrete groups whose multiplier representations are type I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 486-495
- Print publication:
- December 1981
-
- Article
-
- You have access
- Export citation
A distal property of groups and the growth of connected locally compact groups
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 94-98
- Print publication:
- June 1979
-
- Article
- Export citation
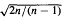 if
if 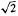 if
if 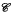 of ℳ. we show that ℳ ⋊
of ℳ. we show that ℳ ⋊ 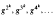 for some positive integer
for some positive integer 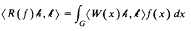
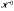 be the space of functions on the Poission boundary ω, of zero mean on ω. When
be the space of functions on the Poission boundary ω, of zero mean on ω. When 